Hello coders! let's suppose we have three numbers n,k,mod=1e9+7 where n,k<=1e9 how to calculate nCk %mod! any hint please! Thanks^__^
→ Pay attention
→ Top rated
| # | User | Rating |
|---|---|---|
| 1 | ecnerwala | 3649 |
| 2 | Benq | 3581 |
| 3 | orzdevinwang | 3570 |
| 4 | Geothermal | 3569 |
| 4 | cnnfls_csy | 3569 |
| 6 | tourist | 3565 |
| 7 | maroonrk | 3531 |
| 8 | Radewoosh | 3521 |
| 9 | Um_nik | 3482 |
| 10 | jiangly | 3468 |
→ Top contributors
| # | User | Contrib. |
|---|---|---|
| 1 | maomao90 | 174 |
| 2 | awoo | 164 |
| 3 | adamant | 163 |
| 4 | TheScrasse | 159 |
| 5 | nor | 158 |
| 6 | maroonrk | 156 |
| 7 | -is-this-fft- | 151 |
| 8 | SecondThread | 147 |
| 9 | orz | 146 |
| 10 | pajenegod | 145 |
→ Find user
→ Recent actions
↑
↓
Codeforces (c) Copyright 2010-2024 Mike Mirzayanov
The only programming contests Web 2.0 platform
Server time: Apr/25/2024 14:35:07 (l2).
Desktop version, switch to mobile version.
Supported by
User lists


| Name |
|---|











You can calculate N! in
O(log(N))using Matrix Multiplication, then calculateN! / [ K! * (N — K)! ] % modHow ? (only when mod is prime)thanks but how to calculate N! in log(n)?
If you can calculate n! in O(log(n)) then you have solved prime checking in O(log3(n)) or something. See this.
so we can calculate n! % mod only using linear solution?
See this. The main idea is sqrt decomposition and Lagrange interpolation. The complexity is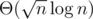 .
.
Thank you so much :)
Doesn't Wilson's theorem give a $$$\mathcal{O}(\log n)$$$ time primality check in that case?
lol no, how you can calculate (p — 1)! % p in log(n)?
The comment I was replying to said " If you could compute $$$n!$$$ in $$$\mathcal{O}(\log n)$$$ you'd have a $$$\mathcal{O}(\log^3 n)$$$ primality check". Note that no claim is made that there is a $$$\mathcal{O}(\log n)$$$ algorithm for computing the factorial.
sorry for carelessness
Another approach is precalculate 106!, (2·106)!, ..., 109! locally and paste it in your code. Then you can easily calculate every factorial using 106 multiplications.
Way 1: Precalculate the factorials. Then, use Fermat's Little theorem, which says that says that $$$a^{-1} \equiv a^{p - 2} \pmod{p}$$$. This allows us to sort of transform modular division into modulo multiplication and then some powers. The pre-computing factorial is $$$O(n)$$$, dealing with the denominator is $$$O(\log(N))$$$ if you use fast exponentiation.
Way 2: Pascal's Identity. Straight forward dynamic programming. This is $$$O(n^2)$$$.
Optimization: Use Lucas's theorem.
I think you didn't realize that $$$n = 10^9$$$ which makes pre computing of factorials $$$O(n)$$$ is impossible within time and memory limit
I was speaking generally, which is why I included Way 2, which is clearly too slow. I think with Lucas's theorem, Way 1 would be sufficiently fast, though.
How would you optimize it using Lucas's theorem?
You can calculate C(n,k) = n! * reverse((n — k)!) * reverse(k!) which reverse(a) = power(a, mod — 2)
If you have enough memory, you can save first a! into an array