I gave a hiring contest yesterday. These are 2 questions i couldn't solve which I think were good problems. If you have any approach to solve these questions within given constraints, Please help.
Q1. Given an N*M matrix with k number of black cells in it. You have to find number of distinct paths from top left (1*1) corner to bottom right corner (n*m) such that each path has atleast one black cell in it. From position (x,y) you can go to (x+1,y) or (x,y+1) only. Positions of all k black cells in matrix are given in input.
N -> number of rows, m -> number of columns, k -> number of black cells
1<=N,M<=10^5, 0<=k<=10^3
Q2. Given a string of parenthesis containing either ')' or '(', you can perform three operations as follows : insert : enter any parenthesis anywhere in string remove : remove any parenthesis from anywhere in string replace : toggle the type of parethesis Now you have to balance the given parenthesis string with minimum number of operations. Output the minimum number of operations used to balance the string.
size -> size of string, 1<=size<=10^6
Note : if P,Q both are balanced then PQ is also balanced and (P) is also balanced.










when and where did this contest happen??
Q1. Suppose we want to go freely, as if there is no black cell or if black cells are not important, from an arbitrary position (x, y) to another position (p, q) with x ≤ p and y ≤ q. Then the number of distinct paths is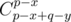 . Now consider the original problem. The path from (1,1) to (N,M) can be broken into 2 stages: going from (1,1) to some black cell without encountering any other black cells before, and then going from that black cell freely to (N,M). Denote f[k], k = 1, 2, ..., K as the number of distinct paths from (1,1) to the black cell k without encountering any other black cells, p[j, k], j = 1, 2, ..., K as the number of distinct paths going freely from black cell j to k. Sort the black cells increasingly by their rows and if two cells are in the same row, by columns. Then f[k] can be computed in O(K2):
. Now consider the original problem. The path from (1,1) to (N,M) can be broken into 2 stages: going from (1,1) to some black cell without encountering any other black cells before, and then going from that black cell freely to (N,M). Denote f[k], k = 1, 2, ..., K as the number of distinct paths from (1,1) to the black cell k without encountering any other black cells, p[j, k], j = 1, 2, ..., K as the number of distinct paths going freely from black cell j to k. Sort the black cells increasingly by their rows and if two cells are in the same row, by columns. Then f[k] can be computed in O(K2):
Having f[k] computed, the rest is simply summing up for all k = 1, 2, ..., K the number of distinct paths going from (1,1) to k first, then from k to (N,M).
Q2. The first step is to remove all the parentheses that are part of a balanced string, which can be done in O(N) where N is the size of the string. We end up with one of the 2 following cases:
Case 1: suppose there are N = 2k parentheses. Toggle the first or the last k parentheses to get a balanced string. The answer is k. If N = 2k + 1, the answer is k + 1.
Case 2: solve each part of the two parts in a similar way to case 1.