Recently, I have come across a problem that need to find a path from $$$S$$$ to $$$T$$$ like these :
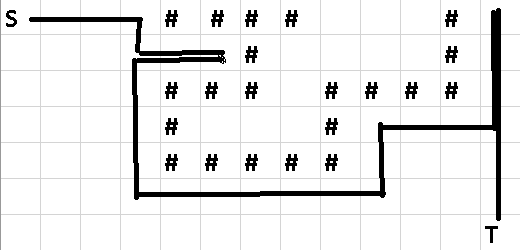
I have tried to do a dfs with order like: up (-1, 0) , right (0, 1), down (1, 0), left(0, -1) (Suppose $$$S$$$ is (1, 1) and $$$T$$$ is (n, m) ). However it fails cases like this
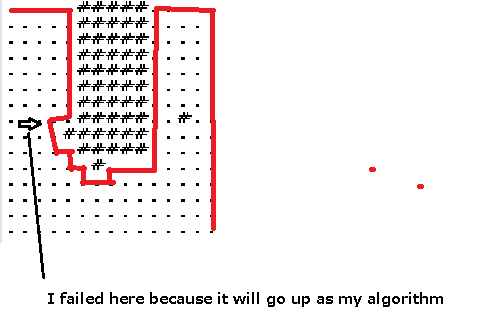
I tried to google it too (but don't know how to use which words to describe this so fail finding anything.). I wonder if there is any algorithm for this.
Thanks anyway <3










Can you elaborate on what you mean by “like these”?
It's like find the cover that is closest to the top border but don't go through the obstacles (#) and go from $$$S$$$ to $$$T$$$.
Actually the problem is : We are given a table if size n * m. Each cell can be the obstacles ( '#' ) or '.' (We can go through this). They told us to find the smallest square that can be put in the table (put on cell '.' only) that will block any path from $$$S$$$ to $$$T$$$.
So the solution is find the upper cover (like the above) and the lower_cover (which is closest to the down border and from $$$S$$$ to $$$T$$$. And put the square so that it intersects with both the upper and lower cover.
Sorry for my poor English !
BFS?
a "left first dfs" will do it. This algorithm works on planar graphs (this is a grid graph and therefore planar). The idea is that you will first try to turn left if thats impossible try to walk straight, than try turning right and then back (order all possible directions cyclic)
Thank you so much ^^