Hello, Codeforces!
Here I'll share an algorithm to solve the classic problem of Range Minimum Query (RMQ): given a static array $$$A$$$ (there won't be any updates), we want to find, for every $$$\text{query(l, r)}$$$, the index of the minimum value of the sub-array of $$$A$$$ that starts at index $$$\text{l}$$$ and ends at index $$$\text{r}$$$. That is, we want to find $$$\text{query(l, r)} = \text{arg min}_{l \leq i \leq r}{\left(A[i]\right)}$$$. If there are more than one such indices, we can answer any of them.
I would like to thank tfg for showing me this algorithm. If you have read about it somewhere, please share the source. The only source I could find was a comment from jcg, where he explained it briefly.
Introduction
Sparse table is a well known data structure to query for the minimum over a range in constant time. However, it requires $$$\Theta(n \log n)$$$ construction time and memory. Interestingly, we can use a sparse table to help us answer RMQ with linear time construction: even though we can't build a sparse table over all the elements of the array, we can build a sparse table over fewer elements.
To do that, let us divide the array into blocks of size $$$b$$$ and compute the minimum of each block. If we then build a sparse table over these minimums, it will cost $$$\mathcal{O}(\frac{n}{b} \log{\frac{n}{b}}) \subseteq \mathcal{O}(\frac{n}{b} \log{n})$$$. Finally, if we choose $$$b \in \Theta(\log n)$$$, we get $$$\mathcal{O}(n)$$$ time and space for construction of the sparse table!
So, if our query indices happen to align with the limits of the blocks, we can find the answer. But we might run into the following cases:
- Query range is too small, so it fits entirely inside one block:

- Query range is large and doesn't align with block limits:

Note that, on the second case, we can use our sparse table to query the middle part (in gray). In both cases, if were able to make small queries (queries such that $$$r-l+1 \leq b$$$), we would be done.
Handling small queries
Let's consider queries ending at the same position $$$r$$$. Take the following array $$$A$$$ and $$$r = 6$$$.
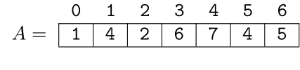
Obviously, $$$\text{query}(6, 6) = 6$$$. Since $$$\text{query}(5, 6) = 5 \neq \text{query}(6, 6)$$$, we can think of the position $$$\text{5}$$$ as "important". Position $$$\text{4}$$$, though, is not important, because $$$\text{query}(4, 6) = 5 = \text{query}(5, 6)$$$. Basically, for fixed $$$r$$$, a position is important if the value at that position is smaller than all the values to the right of it. In this example, the important positions are $$$6, 5, 2, 0$$$. In the following image, important elements are represented with $$$\text{1}$$$ and others with $$$\text{0}$$$.
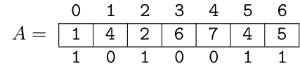
Since we only have to answer queries with size at most $$$b \in \Theta(\log n)$$$, we can store this information in a mask of size $$$b$$$: in this example $$$\text{mask[6] = 1010011}$$$, assuming $$$b \geq 7$$$. If we had these masks for the whole array, how could we figure out the minimum over a range? Well, we can simply take $$$\text{mask[r]}$$$, look at it's $$$r-l+1$$$ least significant bits, and out of those bits take most significant one! The index of that bit would tell us how far away from $$$r$$$ the answer is.
Using our previous example, if the query was from $$$\text{1}$$$ to $$$\text{6}$$$, we would take $$$\text{mask[6]}$$$, only look at the $$$r-l+1=6$$$ least significant bits (that would give us $$$\text{010011}$$$) and out of that take the index of the most significant set bit: $$$\text{4}$$$. So the minimum is at position $$$r - 4 = 2$$$.
Now we only need to figure out how to compute theses masks. If we have some mask representing position $$$r$$$, lets change it to represent position $$$r+1$$$. Obviously, a position that was not important can't become important, so we won't need to turn on any bits. However, some positions that were important can stop being important. To handle that, we can just keep turning off the least significant currently set bit of our mask, until there are no more bits to turn off or the value at $$$r+1$$$ is greater than the element at the position represented by the least significant set bit of the mask (in that case we can stop, because the elements represented by important positions to the left of the least significant set bit are even smaller).
Let's append an element with value $$$\text{3}$$$ at the end of array $$$A$$$ and update our mask.
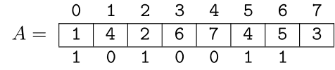
Since $$$\text{A[6] > 3}$$$, we turn off that bit. After that, once again $$$\text{A[5] > 3}$$$, so we also turn off that bit. Now we have that $$$\text{A[2] < 3}$$$, so we stop turning off bits. Finally, we need to append a 1 to the right of the mask, so it becomes $$$\text{mask[7] = 10100001}$$$ (assuming $$$b \geq 8$$$).
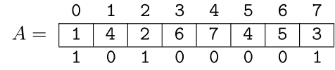
This process takes $$$\mathcal{O}(n)$$$ time: only one bit is turned on for each position of the array, so the total number of times we turn a bit off at most $$$n$$$, and using bit operations we can get and turn off the least significant currently set bit in $$$\mathcal{O}(1)$$$.
Implementation
Here is a detailed C++ implementation of the whole thing.
template<typename T> struct rmq {
vector<T> v; int n;
static const int b = 30; // block size
vector<int> mask, t; // mask and sparse table
int op(int x, int y) {
return v[x] < v[y] ? x : y;
}
// least significant set bit
int lsb(int x) {
return x & -x;
}
// index of the most significant set bit
int msb_index(int x) {
return __builtin_clz(1)-__builtin_clz(x);
}
// answer query of v[r-size+1..r] using the masks, given size <= b
int small(int r, int size = b) {
// get only 'size' least significant bits of the mask
// and then get the index of the msb of that
int dist_from_r = msb_index(mask[r] & ((1<<size)-1));
return r - dist_from_r;
}
rmq(const vector<T>& v_) : v(v_), n(v.size()), mask(n), t(n) {
int curr_mask = 0;
for (int i = 0; i < n; i++) {
// shift mask by 1, keeping only the 'b' least significant bits
curr_mask = (curr_mask<<1) & ((1<<b)-1);
while (curr_mask > 0 and op(i, i - msb_index(lsb(curr_mask))) == i) {
// current value is smaller than the value represented by the
// last 1 in curr_mask, so we need to turn off that bit
curr_mask ^= lsb(curr_mask);
}
// append extra 1 to the mask
curr_mask |= 1;
mask[i] = curr_mask;
}
// build sparse table over the n/b blocks
// the sparse table is linearized, so what would be at
// table[j][i] is stored in table[(n/b)*j + i]
for (int i = 0; i < n/b; i++) t[i] = small(b*i+b-1);
for (int j = 1; (1<<j) <= n/b; j++) for (int i = 0; i+(1<<j) <= n/b; i++)
t[n/b*j+i] = op(t[n/b*(j-1)+i], t[n/b*(j-1)+i+(1<<(j-1))]);
}
// query(l, r) returns the actual minimum of v[l..r]
// to get the index, just change the first and last lines of the function
T query(int l, int r) {
// query too small
if (r-l+1 <= b) return v[small(r, r-l+1)];
// get the minimum of the endpoints
// (there is no problem if the ranges overlap with the sparse table query)
int ans = op(small(l+b-1), small(r));
// 'x' and 'y' are the blocks we need to query over
int x = l/b+1, y = r/b-1;
if (x <= y) {
int j = msb_index(y-x+1);
ans = op(ans, op(t[n/b*j+x], t[n/b*j+y-(1<<j)+1]));
}
return v[ans];
}
};
But is it fast?
As you might have guessed, although the asymptotic complexity is optimal, the constant factor of this algorithm is not so small. To get a better understanding of how fast it actually is and how it compares with other data structures capable of answering RMQ, I did some benchmarks (link to the benchmark files).
I compared the following data structures. Complexities written in the notation $$$<\mathcal{O}(f), \mathcal{O}(g)>$$$ means that the data structure requires $$$\mathcal{O}(f)$$$ construction time and $$$\mathcal{O}(g)$$$ query time.
- RMQ 1 (implementation of RMQ described in this post): $$$<\mathcal{O}(n), \mathcal{O}(1)>$$$;
- RMQ 2 (different algorithm, implementation by catlak_profesor_mfb, from this blog): $$$<\mathcal{O}(n), \mathcal{O}(1)>$$$;
- Sparse Table: $$$<\mathcal{O}(n \log n), \mathcal{O}(1)>$$$;
- Sqrt-tree (tutorial and implementation from this blog by gepardo): $$$<\mathcal{O}(n \log \log n), \mathcal{O}(1)>$$$;
- Standard Segment Tree (recursive implementation): $$$<\mathcal{O}(n), \mathcal{O}(\log n)>$$$;
- Iterative (non recursive) Segment Tree: $$$<\mathcal{O}(n), \mathcal{O}(\log n)>$$$.
The data structures were executed with array size $$$10^6$$$, $$$2 \times 10^6$$$, $$$\dots , 10^7$$$. At each one of these array sizes, build time and the time to answer $$$10^6$$$ queries were measured, averaging across 10 runs. The codes were compiled with $$$\text{O2}$$$ flag. Below are the results on my machine.
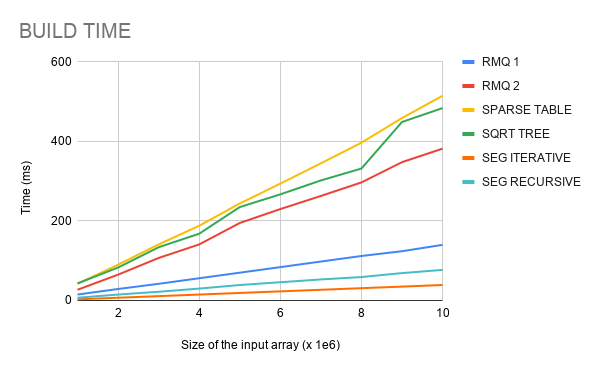
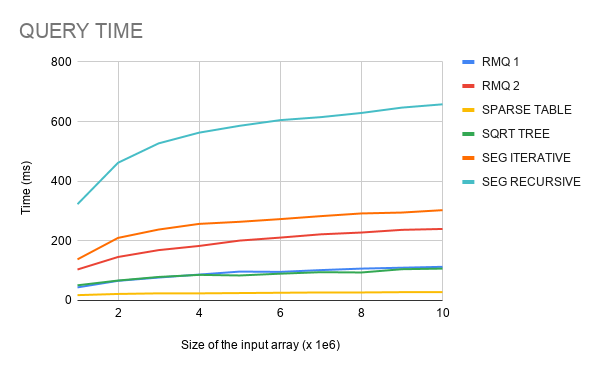
Conclusion
We have an algorithm with optimal complexity to answer RMQ, and it is also simple to understand and implement. With the benchmark made, we can see that its construction is much faster than Sparse Table and Sqrt-tree, but a little slower than Segment Trees. Its query time seems to be roughly the same as Sqrt-tree, losing only to Sparse Table, which have shown to be the fastest in query time.











Well, I've read not about this exactly algorithm but about something similar: Farach-Colton and Bender Algorithm. It can be used to solve an RMQ problem for an array where the distance of any two adjacent elements is exactly one. Maybe it would be interesting for someone :)
Also, if I am not mistaken, the complexity of this algorithm is not exactly $$$O(1)$$$.
__builtin_clzis working in $$$O(b)$$$ where $$$b$$$ is a number of bits of, though the constant factor is really small.From what I could find online, it seems like
__builtin_clztranslates to one or two instructions (source).Not all instructions are actually $$$O(1)$$$. I doubt that
__builtin_clzcan have better complexity that__builtin_popcount, and it is $$$O(b)$$$ (source).Anyway, performance of these operations is quite good, and it doesn't really matter whether it is $$$O(b)$$$ or $$$O(1)$$$
In my implementation I precomputed the most significant bit of every possible mask in an array and chose b as the largest b such 2^b <= N to make it O(1) since I don't trust __ stuff. But I don't think that makes a difference really, it might be even slower since the bottleneck is probably the memory accesses.
As an alternative you could reverse the masks and take the lowest bit, and that can be found with 1 multiplication as mentioned here: https://www.chessprogramming.org/BitScan#De_Bruijn_Multiplication
You are right, it seems to depend on your architecture.
On my machine,
__builtin_clzcompiles to only one BSR assembly instruction and one XOR assembly instruction.Complexity-wise, the algorithm has a $$$\mathcal{O}(n)$$$ construction time only if you assume these operations are $$$\mathcal{O}(1)$$$, and also the size of the word in the architecture can't be smaller than $$$\log n$$$.
What are you guys even talking about? $$$b$$$ is a constant.
Just like log(n) for n fitting in int.
Just like $$$2^n$$$ for $$$n$$$ fitting in int. That’s not what I meant. What I meant is that the discussion here is ill-posed and does not make any sense in this context. If you want to talk efficiency for a function like this, talk in terms of computer cycles (and fix an architecture, because different processors handle the same assembly instruction differently). It’s absurd to take a function that converts to a constant number of ASM instructions and model it in terms of complexity. Maybe the overhead of the cycles scales linearly with the number of bits, but so does addition (unless you assume a infinitely-wide architecture, but probably even with one, as I’m not sure how carrying could be handled). In this sense, clz is not much different than addition.
All in all, I think it depends on what primitives you define to be $$$O(1)$$$. The correct answer, however, in my opinion, is that the algorithm presented has complexity $$$O(n + n/b log(n))$$$ complexity, which falls down to $$$O(n log(n))$$$ on a constant bit architecture. The reply above me (brunomont) seems the most pertinent, while others are just dust in the wind.
I always assume that popcount etc. are $$$O(1)$$$. It's quite common to care about $$$b$$$ in complexity though. There are so many bitset problems where you need $$$/32$$$ factor to pass. Anyway, this discussion happened several times in CF already.
I agree, but in the bitset case we are talking about an algorithm that operates on an (at least theoretically speaking) unbounded "size of input", so analyzing how this algorithm behaves in relation to that size makes total sense.
Here, people are trying to analyze how a sequence of two ASM x86 instructions behaves in relation to the architecture size (I'm not even that's the case, even). See my dilemma?
The Farach-Colton and Bender algorithm is an algorithm for finding LCAs in $$$O(1)$$$ and $$$O(N)$$$ preprocessing. It works by reducing the LCA problem to the easier version of the RMQ (distance of two adjacent elements = 1) and solve that one efficiently.
However, you can still solve the RMQ in $$$O(1)$$$ per query and $$$O(N)$$$ preprocessing with the Farach-Colton and Bender algorithm (for any array), if you first build a Cartesian tree over the array. Then every RMQ in the array corresponds to a LCA query in the Cartesian tree.
brunomont If you want to add the Farach-Colton and Bender variation to your benchmark: https://pastebin.com/h5X9eFsB Even though it has optimal complexity, it's speed is really bad. Preprocessing is terribly slow, and answering queries is also not good. Definitely not a winner...
Thank you for sharing that implementation! However, it has performed so poorly that I don't think it makes sense to add it to the benchmark (build time was about 3x larger than the sparse table, and query time was slower than the iterative segment tree).
Isn't it: query(6, 6) = 5 query(5, 6) = 4 query(4, 6) = 4
We are trying to find the index of the minimum. =)
Ohhh I get it. I was confused, thanks!
I think this is The Fischer-Heun Structure as mentioned in here: https://web.stanford.edu/class/cs166/lectures/01/Small01.pdf
The name is given on slide 74.
This is not the same algorithm, although it uses the same idea to divide the array into blocks of size $$$\Theta(\log n)$$$ and build a sparse table out of those blocks. "Small" queries are handled in a different way.
It's nice to see a rmq implementation that is both easier and much faster than the usual linear time one based on enumerating cartesian trees. I guess it's time to replace this monstrocity (a different complicated algorithm based on lca).
Since you've separated queries from building, it would be interesting to know how may queries you need for a fixed $$$n$$$ (say $$$n=10^5$$$ or $$$n=10^6$$$) so that rmq1 is faster than iterative segtrees or that the sparse table is faster than rmq1.
I was going to ask why you're only using $$$b=30$$$, but then I saw that you used $$$b=64$$$ in the benchmark.
msb(at&-at)could be replaced with something using__bultin_ctzll, which might give you a tiny speedup.Can you do this with long long?
Also is it possible to implement gcd or other things like that?