Hello everyone!
JOI Open Contest 2020 will be held from Sunday, September 6, 04:00 UTC to Monday, September 7, 04:00 UTC. You can start at any time and the duration is basically 5 hours. Note that the duration becomes shorter if you start after Sunday, September 6, 23:00 UTC, i.e. less than 5 hours before the contest ends.
There will be 3 tasks. Each submitted source program must be written only in C++. Problem statements will be provided both in Japanese and in English. You can find more details in the contest page.
Past contests are also available in this page. Since the judge server isn't available now, please download testcases when you want to test your code.
Good luck and have fun!










You can solve past problems here: https://oj.uz/problems/source/53
You can solve all problems here: https://oj.uz/problems/source/530
Can someone share proof of these claims of problem B.Monochrome ?
let a be the list of black points in sorted order
let b be the list of white points in sorted order
there exists a optimal solution in which there is a line from each a_i to b_((i+k)%n) for some 0<=k<n
let c_i be the number of intersections when k=i
there exists a cyclic shift of array c such that it is ternary
Is claim 2 really correct?
I didn't implement my solution but I think that claim 1 is correct and then we need to $$$O(n)$$$ times add a linear function $$$f(i)=i+const$$$ or $$$f(i)=-i+const$$$ to an interval of indices of white points. That's because for every black point the number of intersections of its segment is $$$min(pointsAbove, pointsBelow)$$$ like square1001 described below. If I'm correct, maybe this helps in proving your bitonicity claim.
I asserted the claim 2 on the test data of the first 3 subtasks and the samples and it worked.So I coded it up efficiently and it got 100.I believe the test data is strong only.
Would you please describe your 100 points solution?
after claim 1 there are only O(n) solutions. Checking each of them can be done in O(nlogn) so total complexity will be O(n*n*logn) which gets 35 points claim 2 means that the array c(with reference to first comment) is bitonic there are 2 cases if c_0>=c_n-1: binary search for the last index i such that c_i>=c_0 and then to calculate the answer by ternary search in the range (0,i) else: binary search for the first index i such that c_i>=c_n-1 and then to calculate the answer by ternary search in the range (i,n-1)https://oj.uz/submission/293453
Now you can find a proof in the editorial, though it is a bit long.
Problem 2 "Monochrome Points" was superb. It was very difficult but interesting.
Maybe I solved with an approach which is very different from others.
First, think about maximizing the total length of arcs for each line, instead of maximizing the number of intersections of lines. Here, we define length of arc between point $$$x$$$ and $$$y$$$, the value of $$$\min(|x - y|, 2N - |x - y|)$$$.
If the maximum total length of arcs is $$$X$$$, always, the answer will then be $$$(X - N) \div 2$$$. Note that this formula is not necessarily true for all ways of matching, but it is always true for maximum pattern. The idea of proof is that, in maximum pattern, lines with arc length $$$L$$$ is always passed by other $$$L-1$$$ segments.
The line will divide the circumference of circle into two. This time we call them "smaller part" and "larger part".
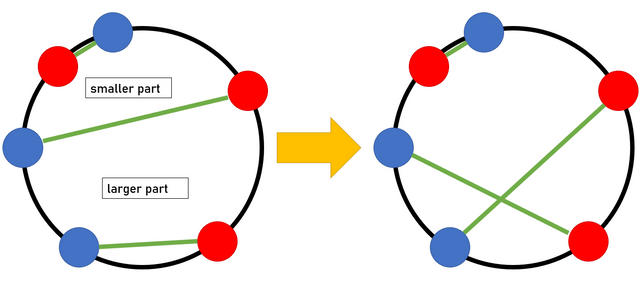
Suppose that there is a line $$$d$$$ (of arc length $$$L$$$) which is passed by other $$$L-2$$$ segments or less. Then, always, there are at least one line which does not cross with $$$d$$$, for both smaller part and larger part.
(Note that black/white of points is translated to red/blue because of visual matters)
As seen in the picture above, we see three lines; one is $$$d$$$, and the other is a line in smaller part and in larger part. The order of color from left to right is either "red — blue" or "blue — red". Since there are three segments, "two red-blue lines" or "two blue-red lines" exists, which have potential to increase the total length of arcs by crossing these lines.
This contradicts that the total length of arcs is maximal. That's why the line is passed by $$$L-1$$$ other segments. This proof yields that the maximum number of intersections can be computed as $$$(X-N) \div 2$$$.
This means we need to calculate $$$X$$$ in a reasonable time. Since this problem is Maximum Weight Matching of bipartite graph, we can calculate in $$$O(N^3)$$$ time with Hungarian Algorithm. This solution yields 25 points by subtask 1 and 2.
However, to solve it more quickly, we need to devise more. Here, the maximization of total length is difficult. Let's think about minimization of total length instead! We can transform from "maximize-problem" to "minimize-problem" by transferring all $$$N$$$ white points to the opposite position in the circle.
The minimization problem is easier. If we cut one points in circumference in circle, then the circle is developed to "a segment" with length $$$2\pi r$$$. The "minimize-problem" for 1D line is a classic problem (the idea can be used in AtCoder Problem "1D Matching"), and can be solved in linear time. Since we brute-force cutting points of circumference, the total time is $$$O(N^2)$$$.
Using a data structure, this can be improved to $$$O(N \log N)$$$. Thank you for reading!
Actually I just reduced the number of candidate solutions to $$$O(N)$$$ (each of which can be checked in $$$O(N\log N)$$$ or I think even $$$O(N)$$$ time but I was lazy to optimize). Then, I just printed out values for small $$$N$$$ and realized it was somehow bitonic so I just did a binary search and passed it without much effort hmm (though I didn't prove the property).
How to solve C (Power Plant)?
Observe that there can only be one pair of turned on generators $$$x, y$$$ such that $$$y$$$ is a parent of $$$x$$$. If there is more than one pair, then there exists a triple $$$x, y, z$$$ such that $$$y$$$ is along the path from $$$x$$$ to $$$z$$$, and will be turned off.
Then, let $$$dp[u]$$$ = max profit in the subtree of $$$u$$$ such that no generator that is turned on is a parent of another.
The transitions are:
where $$$gen(u)$$$ denotes whether $$$u$$$ is a generator (if it is, it will be turned off, giving $$$-1$$$ profit).
The answer equals:
because you can choose to have one generator to be the parent of another.
Submission
I'm understand, Thanks bro!
I think test cases for furniture are weak. My O(nm(n+m)) soln passes in 0.5s.
https://github.com/T1duS/CompetitiveProgramming/blob/master/Olympiad/JOI/oc20_furniture.cpp
When will the editorial be realeased?
The editorial has already been released. See the Reviews section of the contest page.