You are given following:- - an array A consisting of N positive integers - Q queries of the form L,R,M
consider all subsequences of subarray from L to R of size M.
Determine the sum of Bitwise OR of all these subsequences. Bitwise OR of an empty subsequence is 0. If there is no Subsequence of Length M, print 0.
- print the output with mod 998244353.
- A subsequence is a sequence that can be derived from the given sequence by deleting 0 or more elements without changing the order of the remaining elements.
- 1 based indexing is followed.
Example A=[1,2,3] Q=[1,3,2] // L,R,M
subarray= [1,2,3] for this we have 3 subsequences of length 2. - [1,2] [2,3] [1,3]
Bitwise OR of all above subsequences is 3+3+3=9 , so output is 9
constraints as below
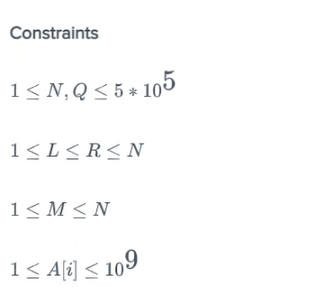











Operate on each bit separately. For ith bit = ((r-l+1,m)-(# off bits,m))*2^i , where (a,b) is binomial coefficient.
Hi could you elaborate little more? i m kind of beginner, so could not connect much. may be small example would be useful. thanks
Let's rephrase this problem , consider a binary sequence [0,0,0,1,1,1] how many sub sequences exist of a given sequence having length m such that it contains at least single 1 ?? (# sub sequence of length m — # sub sequence containing only 0)