td,dr: A 900, B1 1000, B2 1100, B3 1300, C1 1200, C2 1400, D1 1600, D2 1700, D3 2200, E1 1800, E2 2100.
Have you been wondering what is the difficulty of Code Jam problems on a codeforces scale? me too.
I made an estimate for the 2021 qualification round (link), and I plan to do it also for the upcoming rounds. This is the best estimate I came up with, but I am sure it's possible to do better. I share here the process and the results, and I welcome any feedback.
Data
I use two data sources:
CJ contest result data, downloaded using vstrimaitis code, see details in his great blog post. From here I get the list of contest participants and what problems they solved.
CF users data, downloaded using CF API. From this, I get the current rating of every CF coder.
I assume that many coders use the same username across different platforms. If for a given CJ contestant I find a CF user with the same name (case insensitive), I assume they are the same person.
I assign to each CJ participant the rating of the corresponding CF coder, and I discard all other participants. This filter may introduce some bias, but I don't see better solutions.
Difficulty Estimation 1: The 50% Bucket
Method
The formula used by CF to determine the difficulty of a problem is not public. However, the main idea is that you have a 50% probability of solving any problem with difficulty equal to your rating. Some details here.
I divide contestants into buckets wide 100 rating points (a 1450 and a 1549 coders fall in the 1500 bucket), and I see what bucket had a 50% rate of success. That's my estimate of the difficulty of the problem. I group together all ratings above 3000 and below 500, or the sample size would be way too small.
Results
Out of the 37,398 contestants who submitted something during the qualification round, 11,109 have a homonym CF user. Here their success rate on the different problems: 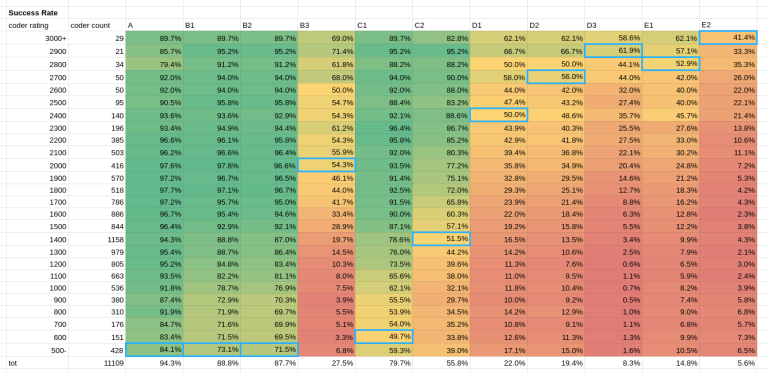
Estimated Difficulty:
A <=500, B1 <= 500, B2 <= 500, B3 2000, C1 600, C2 1400, D1 2400, D2 2700, E1 2600, E2 3000.
Issues
Difficulties don't look right. B3 is a simple dp problem, definitely not 2000 difficulty. What is going wrong then?
One obvious issue is that I am matching profiles across platforms using the username, which is probably introducing noise. But I don't see much better options.
Another big issue is that many contestants didn't seem to care about solving all the problems. See LHiC for example, an international grandmaster who just solved problems E1 and E2. My guess of what is happening: since this is a qualification round where you only need a certain sum of points to pass, many people just thought that solving all the problems wasn't worth the time. This lowers the problem success rate and inflates the difficulty.
Difficulty Estimation 2: Inverse Prob Function
Method
For this round, I want to exclude from my estimation the data for top coders, who didn't bother solving all the problems. Bottom contestants also come with some issues. For example, some low-rated contestants seem to be just the new profile of a seasoned coder, so we can see coders with a rating below 1000, few CF contests, but who solved all the problems.
If I exclude all this data, I can't apply the bucket method above anymore, since for many problems there is no rating bucket who had a 50% success rate. What can I do with the remaining average coder data?
Well, according to CF rating system, if your rating is R, and the difficulty of a problem is D, then your probability of solving it is $$$p=\frac{1}{1+10^\frac{D-R}{400}}$$$.
We know the contestants rating, their rate of success, so we can estimate the difficulty of the problem by inverting the formula: $$$D=400 \cdot \log_{10} \left( \frac{1-p}{p} \right) + R$$$.
I decided to look only at contestants around the mode of the rating distribution, $$$1400 \pm 100$$$. This leaves about 3,000 contestants.
Results
Below the difficulties I obtained with this method:
A 878, B1 1020, B2 1050, B3 1634, C1 1158, C2 1395, D1 1682, D2 1727, D3 1968, E1 1784, E2 1979.
This feels more reasonable to me.
I do some further rounding, in some cases arbitrarily up or down where I felt it was needed. For example, D1 1682 and D2 1727 would both fall on 1700, but they are definitely on a different level, so I round the former down.
Adjustments
Thanks for the feedback, practicener and Ahmadsm2005.
I lowered B3, to be below C2. Probably the fact that it was worth only 1 point during the contest resulted in many coders skipping the test, lowering the success rate and inflating the difficulty.
I also increased E2 to 2100 and D3 to 2200. The approach of inverting the prob function doesn't seem to work very well for difficulties far away from the rating of the contestants I chose as a reference, 1400.
Final Estimate
A 900, B1 1000, B2 1100, B3 1300, C1 1200, C2 1400, D1 1600, D2 1700, D3 2200, E1 1800, E2 2100.
What are your thoughts?











Auto comment: topic has been updated by areo (previous revision, new revision, compare).
The estimations seem okayish, but C2 was definitely way harder than B3. Problem B was ...........a bit standard? Well, again this is subjective and it may vary with people. E2 was more like 2100+. A lot of experienced participants seemed to take time on it.
Thanks for the input.
I agree on C2 vs B3. I think the issue there is that B3 gave only 1 point, vs 11 points for C2. I imagine many people didn't have enough incentive to bother solving B3, lowering the problem success rate. I wouldn't know how to adjust for it tho.
On E2 being 2100+, I can believe you. It is above my rating so I don't have a good feeling for how much above 2000 to place it.
My impression is that inverting the probability function doesn't work that well for problems far away from the contestant ability. But again, I wouldn't know how to adjust for it.
D3 was tricky not gonna lie. Deserve around 2100's? E2 was easier than D3 I think.