humblefOOOol's blog

Little Help in Bridge tree problem?
By humblefOOOol, history, 3 years ago, In English

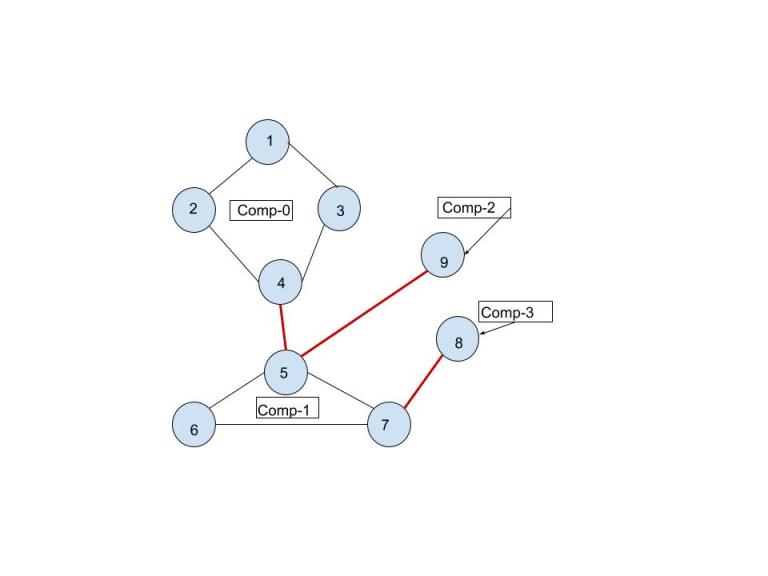
After constructing bridge tree, we have bi-connected components as nodes and bridges as edges. Is there any possible way to print every bicomponent which is a node in bridge tree.

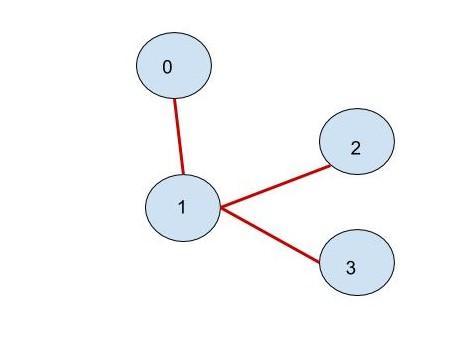
eg:

Graph0

Its bridge tree is

d3e57dcd3f3621f14afc8bb36c98614c604d73ee

Can we print all biconnected components from bridge tree itself?

Here in the above graph : Comp1 -> (1-2-3-4) Comp2--> (5-6-7) Comp3-->(5-9) Comp4---> (7-8)

  • Vote: I like it
  • -7
  • Vote: I do not like it

»
3 years ago, # |
  Vote: I like it +8 Vote: I do not like it

Auto comment: topic has been updated by humblefOOOol (previous revision, new revision, compare).

→ Reply
»
3 years ago, # |
  Vote: I like it +1 Vote: I do not like it

Can any one help in this problem. Its from cf blog https://codeforces.com/blog/entry/83980#:~:text=2%2Dedge%20connected%20component%20in,have%20any%20bridges%20in%20it.

→ Reply
»
3 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Not exactly sure what your question is, do you mean recover

Comp1 -> (1-2-3-4) Comp2--> (5-6-7) Comp3-->(5-9) Comp4---> (7-8)

from just looking at the graph? The IDs 1, 2, 3, 4 are just arbitrary numbers representing the components, there's no special connection between the number 1 and the set [1, 2, 3, 4]. If you mean recovering the original nodes after building the bridge tree, you could just store them in a 2D vector when building.

→ Reply
  • »
    »
    3 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Yes I am maintaining a 2 -d vector but in this example I am not able to retrieve all components

    My sample code

    const int MAXN = 1e5 + 5; const int MAXM = 1e5 + 5;

    int N, M, timer, compid;

    vector<pair<int, int>> g[MAXN]; bool used[MAXN], isBridge[MAXM]; int comp[MAXN], tin[MAXN], minAncestor[MAXN];

    vector tree[MAXN]; // Store 2-edge-connected component tree.(Bridge tree).

    void dfs(int v, int p) { tin[v] = minAncestor[v] = ++timer; used[v] = 1; for(auto &e: g[v]) { int to, id; tie(to, id) = e; if(to == p) continue; if(used[to]) { minAncestor[v] = min(minAncestor[v], tin[to]); } else { dfs(to, v); minAncestor[v] = min(minAncestor[v], minAncestor[to]); if(minAncestor[to] > tin[v]) { isBridge[id] = true; } } } }

    void dfs1(int v, int p) { used[v] = 1; comp[v] = compid; for(auto &e: g[v]) { int to, id; tie(to, id) = e;

    if(isBridge[id]) { // avoid traversing from this edge. so we get full component.
        continue;
    }
    if(used[to]) {
        continue;
    }
    dfs1(to, v);
}

    }

    vector<pair<int, int>> edges;

    void addEdge(int from, int to, int id) { g[from].push_back({to, id}); g[to].push_back({from, id}); edges[id] = {from, to}; }

    void initB() {

    for(int i = 0; i <= compid; ++i)
    tree[i].clear();
for(int i = 1; i <= N; ++i)
    used[i] = false;
for(int i = 1; i <= M; ++i)
    isBridge[i] = false;

timer = 0;
compid = 0;

    }

    void bridge_tree() {

    initB();

dfs(1, -1); //Assuming graph is connected.

for(int i = 1; i <= N; ++i)
    used[i] = 0;

for(int i = 1; i <= N; ++i) {
    if(!used[i]) {
        dfs1(i, -1);
        ++compid;
    }
}

for(int i = 1; i <= M; ++i) {
    if(isBridge[i]) {
        int u, v;
        tie(u, v) = edges[i];
        // connect two componets using edge.
        tree[comp[u]].push_back(comp[v]);
        tree[comp[v]].push_back(comp[u]);
    }
}

    }

    void init() { edges.clear(); edges.resize(M + 1); for(int i = 1; i <= N; ++i) g[i].clear(); }

    void solve() { cin >> N >> M;

    init();

for(int i = 1; i <= M; ++i) {
    int u, v;
    cin >> u >> v; addEdge(u, v, i);
}

bridge_tree();

    }

    → Reply
    • »
      »
      »
      3 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Here when i am creating a tree when i am trying to retrieve those components its not working

      → Reply
      • »
        »
        »
        »
        3 years ago, # ^ |
        ← Rev. 2   Vote: I like it 0 Vote: I do not like it

        In your DFS method, you can maintain a stack holding all the nodes you visit, then whenever you encounter a bridge, continuously pop nodes off the stack until you pop off an endpoint of the bridge, and all nodes you just popped off will form a component in the bridge tree. It's easier to just show code:

        Click Me

        If at the end of the DFS your stack isn't empty, then all remaining nodes in the stack form the last component.

        → Reply
        • »
          »
          »
          »
          »
          3 years ago, # ^ |
            Vote: I like it 0 Vote: I do not like it

          Thank you so much. It absolutely worked. What if we create a block-cut tree. is it the same to retrieve the bcc from there too?

          → Reply
          • »
            »
            »
            »
            »
            »
            3 years ago, # ^ |
              Vote: I like it 0 Vote: I do not like it

            Yea, just pop from the stack at each articulation point instead of bridge.

            → Reply