kushal.p1699's blog

Generating Subsets (Recursion)
By kushal.p1699, history, 3 years ago, In English

Hi all, I'm so excited to write my first blog here.

Last week I was helping my friend in tracing the recursion problem called Generating subset. He had the code snippet, but he was not able to understand the flow of the program. So, I tried to explain the logic to him. I'm happy that, my explanation made him clear on his doubts. I thought of sharing my explanation on tracing this problem by writing a new blog.

Problem statement:
Generate the subsets of given N elements using recursion.

Input:
1 2 3

output:
1 2 3
1 2
1 3
1
2 3
2
3

Explanation:
Subsets of [1,2,3] is null, {1}, {2}, {3}, {1, 2}, {1, 3}, {2, 3}.

code: 

#include <bits/stdc++.h>
using namespace std;

vector<int> subset;
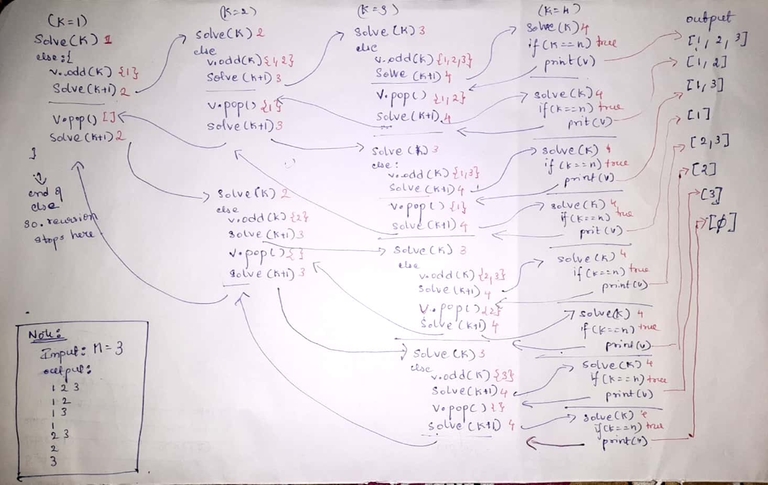
void solve(int a[], int n, int index) {
    if(index == n){
        // print the subset
        for(int i=0; i<subset.size(); i++){
            cout << subset[i] << " ";
        }
        cout << "\n";
    }else{
        subset.push_back(a[index]);
        solve(a, n, index+1);
        subset.pop_back();
        solve(a, n, index+1);
    }
}

int main() {
    int a[] = {1, 2, 3};
    int n = sizeof(a)/sizeof(a[0]);
    int startIndex = 0;
    solve(a, n, startIndex);
    return 0;
}

My explanation of this program is given below.

This is my first blog ever in my life. If you find any mistakes or you have any suggestions, please let me know. So that I can improve it form next time.

Thank you.

  • Vote: I like it
  • +33
  • Vote: I do not like it

Comments Comments (16)
| Write comment?
»
3 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Can you please tell us what is the time complexity? O(n^2)?

→ Reply
  • »
    »
    3 years ago, # ^ |
      Vote: I like it +2 Vote: I do not like it

    Should be $$$O(2^n)$$$ as there are $$$2^n$$$ subsets..

    → Reply
    • »
      »
      »
      3 years ago, # ^ |
        Vote: I like it +15 Vote: I do not like it

      I hate to be that guy but shouldn't the complexity be $$$O(n \cdot 2^n)$$$? We have to generate and print each subset.

      → Reply
»
3 years ago, # |
  Vote: I like it -13 Vote: I do not like it

Dude you are just a noobie. No one is going to take this blog seriously due to that. This is a very basic concept, everyone on CF already knows this.

→ Reply
  • »
    »
    3 years ago, # ^ |
      Vote: I like it +12 Vote: I do not like it

    You're one to talk, being unrated and all

    → Reply
»
3 years ago, # |
  Vote: I like it +13 Vote: I do not like it

I appreciate your efforts but this is like Leetcode and GeeksForGeeks article, better be there, don't take it harshly.

→ Reply
»
3 years ago, # |
  Vote: I like it +4 Vote: I do not like it

Looks like there's a typo in the code: subset.push_back(a[index)]; shouldn't the ) and ] be switched around?

→ Reply
»
3 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Hey, Can anyone tell me which is the efficient way to solve this problem?

→ Reply
  • »
    »
    3 years ago, # ^ |
      Vote: I like it +14 Vote: I do not like it 
    for (int i=0; i<(1<<n); i++) {
        vector<int>subset
        for (int j=0; j<n; j++) {
            if (i&(1<<j)) {
                subset.push_back(j);
            }
        }
    }
    → Reply
  • »
    »
    3 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    That's the most efficient way, $$$O(N \cdot 2^N)$$$ is the theoretical limit, because you have to print out $$$N \cdot 2^{N-1}$$$ numbers total (each number is part of $$$2^{N-1}$$$ subsets).

    But the thing about this recursive approach is it's slower to write in a competition. So what many people (including me) do is use binary numbers:

    You have an array $$$a$$$ with length $$$n$$$. Generate all binary strings of length $$$n$$$, and call the $$$i$$$'th one $$$b_i$$$. Generate the subset by including the $$$j$$$'th number if the $$$j$$$'th bit of $$$i$$$ (or the $$$j$$$'th character of $$$b_i$$$) is a $$$1$$$. This technique is commonly called a bitmask.

    I believe that although this way has the same time complexity, $$$O(N \cdot 2^N)$$$, it has a lower constant factor than the recursive approach.

    An example of code for this:

    PS: Bitmasks are often useful if you're partitioning an array into two disjoint arrays, so a $$$0$$$ at position $$$i$$$ means $$$a_i$$$ goes into the first array, and a $$$1$$$ means $$$a_i$$$ goes into the second array.

    → Reply
»
3 years ago, # |
  Vote: I like it +4 Vote: I do not like it

When I was beginner, this was nightmare for me to understand

→ Reply
»
23 months ago, # |
  Vote: I like it +23 Vote: I do not like it

No offense but understanding recursion by like this or by drawing tree diagrams is literally gonna blow your head, as it would be way complicated. When I was a beginner, I found understanding recursion via this approach a nightmare.

A better way would be to assume, whenever a function gets called inside another function again, that your subproblem is somehow magically solved (and thus stop going deeper into recursion or you're gonna get confused). Then, after solving subproblems, you devise a way to "combine" them to solve the "bigger" problem.

→ Reply
»
15 months ago, # |
  Vote: I like it +1 Vote: I do not like it

Thanks bro for explanation. It helped me

→ Reply
»
4 weeks ago, # |
  Vote: I like it 0 Vote: I do not like it

I am really noob to CP. I am having a hard time understanding this code. Why does 'k' turns to 2 after reaching 3?

→ Reply
  • »
    »
    4 weeks ago, # ^ |
    ← Rev. 2   Vote: I like it 0 Vote: I do not like it

    it doesn't return to, it's another stack of recursions

    this code works as follows:

    image

    either an element comes or doesn't, in the else part, it handles when we haven't visited every element, the first 2 lines of the else part are when it comes, and the second 2 lines are when it doesn't. bcuz of the way recursion(in total stack memory) works, it starts drawing it from above, not equally every where, so it first finishes writing 123, then goes to the last time it got branched and solves there etc

    it's just understanding recursions

    → Reply