1) Because of small constraints, just iterate n from 1 to Tn and check 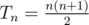
2) Let's consider a graph, where the letters A, B, C are the vertexes and if x < y, then the edge y - > x exists. After that let's perform topological sort. If a cycle was found during this operation, put "Impossible" and exit. Otherwise put the answer.
Another approach is acceptable because of small constaints (by Connector in russian comments).
Just iterate over all of 3! permutaioins of the letters and check if they are sorted. If no such permutation, put "Impossible"
3) Let's iterate over all of 6! = 720 permutations. For every permutation let's try to put the first 3 words horizontally, the others - vertically:
A Conditions for the solution existence
Note In C++ if you use vector<vector<char> > or vector<string> as the field type, then you can simply use operator "<" for updating.
4) Let's consider not the most efficient, but AC algorithm, with the complexity O(mCn5log(Cn5)).
Let's consider the 1 answer of the system: <number, v>. The amount of the variants of the password is Cnv - not very large number in constaints of the problem, you can simply generate this variants. Declare this set of variants as current. Now, for the every answer let's generate a set of possible passwords, and let's declare the intersection of this set and current set as current. After m iterations we'll have some set. Then we'll erase elements from this set, which were in the answers of the system, and the answer of the problem will be the size of this set.
5) Let's consider an algorightm with complexity O((n + m)log(n + m)).
Exclude from considiration every wall can't be achieved by canon: x > v2 / g
Because of α < =π / 4:
Sort walls by x. Now the initial problem has reduced to the problem: for every shoot it is need to obtain minimal index of the wall, when shoot angle is between attack angles for this wall. This problem can be solved by Segment Tree for Minimum with possibility to update on an interval. At first, fill tree with KInf. Next, for every wall let's perform update(α1, α2, index). Then let's iterate over requests. If getMin(α) == KInf, then missle do not hit any wall and hit the land, otherwise it hit the wall with index getMin(α).
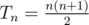
for (int n = 1; n <= Tn; n++)
{
if (n * (n + 1) / 2 == Tn)
{
cout << "YES\n";
return;
}
}
cout << "NO\n";
2) Let's consider a graph, where the letters A, B, C are the vertexes and if x < y, then the edge y - > x exists. After that let's perform topological sort. If a cycle was found during this operation, put "Impossible" and exit. Otherwise put the answer.
Another approach is acceptable because of small constaints (by Connector in russian comments).
Just iterate over all of 3! permutaioins of the letters and check if they are sorted. If no such permutation, put "Impossible"
3) Let's iterate over all of 6! = 720 permutations. For every permutation let's try to put the first 3 words horizontally, the others - vertically:
- hor[0], ver[0] - left-up
- hor[2], ver[2] - right-down
- hor[1]: (len(ver[0]) - 1, 0)
- ver[1]: (0, len(hor[0]) - 1)
A Conditions for the solution existence
- len(hor[0]) + len(hor[2]) == M + 1 // edges of "eight"
- len(ver[0]) + len(ver[2]) == N + 1 // edges of "eight"
- len(hor[0]) >= 3 && len(hor[2]) >= 3 && len(ver[0]) >= 3 && len(ver[2]) >= 3 // "eight" is nondegenerate
- The letters at start/end of appropriate strings are match
- The letters on the intersection of hor[1], ver[1] are match
Note In C++ if you use vector<vector<char> > or vector<string> as the field type, then you can simply use operator "<" for updating.
4) Let's consider not the most efficient, but AC algorithm, with the complexity O(mCn5log(Cn5)).
Let's consider the 1 answer of the system: <number, v>. The amount of the variants of the password is Cnv - not very large number in constaints of the problem, you can simply generate this variants. Declare this set of variants as current. Now, for the every answer let's generate a set of possible passwords, and let's declare the intersection of this set and current set as current. After m iterations we'll have some set. Then we'll erase elements from this set, which were in the answers of the system, and the answer of the problem will be the size of this set.
5) Let's consider an algorightm with complexity O((n + m)log(n + m)).
Exclude from considiration every wall can't be achieved by canon: x > v2 / g
Because of α < =π / 4:
- Function Xmax(α) is monotonous
- Function Y(α, x), when x is fixed, is monotonous
Sort walls by x. Now the initial problem has reduced to the problem: for every shoot it is need to obtain minimal index of the wall, when shoot angle is between attack angles for this wall. This problem can be solved by Segment Tree for Minimum with possibility to update on an interval. At first, fill tree with KInf. Next, for every wall let's perform update(α1, α2, index). Then let's iterate over requests. If getMin(α) == KInf, then missle do not hit any wall and hit the land, otherwise it hit the wall with index getMin(α).











I did some pretty hardcore implementation in Div2B "so called proper brute force" can't be more brute have a look 60172369
We can see this problem as a directed graph, so we have to ensure that the following condition should be veryified to have an answer:
1. Every node in the graph should have not one degree at the same time.
2. There are no bidirectional edges.
With the first condition we ensure that there isn't a cycle, with the second we don't have a contradiction.
My sub: 60185706