First post on Codeforces. I hope you enjoy it.
Codeforces Round #215 (Div. 1) Problem C — Sereja and the Arrangement of Numbers
Analysis
Treat each q[i] as vertex, and treat each pair of a[j] and a[j+1] as an edge. What we need is a semi-Eulerian graph in which multiple edges are allowed between two edges, and each vertex must be connected to another by at least one direct edge. 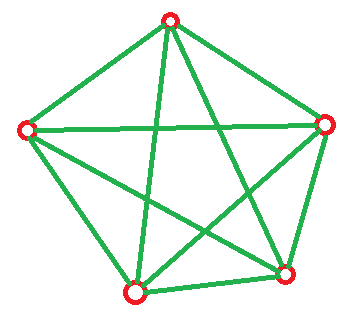
Situation for 5 vertexes, which can afford edges not less than 10.
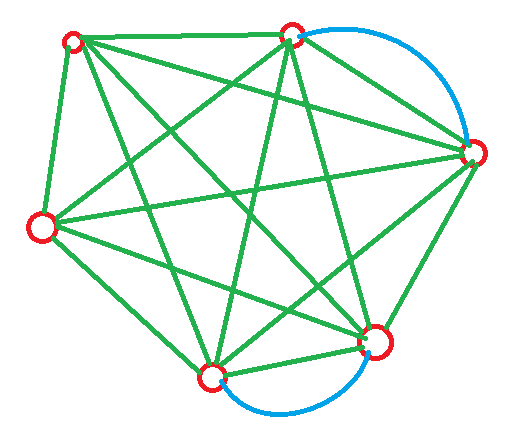
Situation for 6 vertexes, which can afford edges not less than 17.
Solve
First, calculate the maximum number of q[i]s that are available for the limit of number of edges, store it into N. Second, sort the w[] in a descending order, pick N largest costs, the sum of which is the answer.
Notice
For each given n, there are n-1 instead of n edges that are available in the graph: a[1]-a[2], a[2]-a[3], a[3]-a[4], ... , a[n-1]-a[n].
Code
#include<algorithm>
#include<cstdio>
#include<iostream>
using namespace std;
long long calc(long long limit, long long sup)
{
long long inf = 1;
while(inf < sup)
{
long long mid((inf + sup + 1) >> 1);
// for odd vertexes, the complete graph is what we need
if(mid & 1)
{
long long temp(mid * (mid - 1) >> 1);
if(temp <= limit)
inf = mid;
else
sup = mid - 1;
}
// for even vertexes, the complete graph is not semi-Eulerian
else
{
// we need to add some edges to make it semi-Eulerian
long long temp((mid * (mid - 1) >> 1) + (mid / 2 - 1));
if(temp <= limit)
inf = mid;
else
sup = mid - 1;
}
}
return inf;
}
long long value[100010];
bool cmp(long long x, long long y)
{
return y < x;
}
int main()
{
long long n, m;
scanf("%I64d%I64d", &n, &m);
n = calc(n - 1, m);
// replaces n with the result
for(long long i(0); i != m; ++i)
{
long long x;
scanf("%I64d%I64d", &x, value + i);
}
sort(value, value + m, cmp);
long long ans(0);
for(long long i(0); i != n; ++i)
ans += value[i];
printf("%I64d\n", ans);
}











So, in the case of an even node count, how can we prove that we need to add at least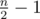 edges so that the graph becomes semi-Eulerian? And how do we prove that this is always possible?
edges so that the graph becomes semi-Eulerian? And how do we prove that this is always possible?
If the graph is semi-Eulerian, than every vertex (maybe except two of them) is of even degree.
If k is even, then there are exactly k vertices with odd degree. If you add an edge, than, obviously, not more than two vertices can change their degree from odd to even. So, you need to add at least (k — (k-2)) / 2 = k-1 edges.
It is sufficient, because you can add edges 1-2, 3-4, ..., k-4 — k-3.
Oh okay, I didn't know that theorem about semi-Eulerian graphs. Thanks a lot.
very nice proof. thanks a lot! :)
A graph is semi-Eulerian iff the number of nodes with odd degree is at most 2. In the case of a complete graph on n vertices, where n is even, initially all nodes have odd degree. If you add a edge to the graph, the number of nodes with odd degree will not decrease by more than two. On the other hand, if you connect two nodes which have odd degree, it will decrease by two. So the optimal way to add a minimum number of edges to the graph and make it semi-Eulerian is to connect pairwise the vertices with odd degree (all but two).
Thanks! Makes a lot of sense.
This can actually be interpreted as "Count the minimum number of paths to travel through all edges such that each edge is crossed exactly once" (then we simply add duplicating edges to connect these paths).
Degrees of nodes in each path decrease by an even number except for the first and the last (they can be the same). Hence, at most we can reduce the number of odd-degreed nodes by 2 with one path. When n is even, we need n / 2 paths which means n / 2 - 1 duplicating edges.
When n is even, there're n odd nodes. One multiple egde can make two of them become even. To get the minium ans we just let two points stay odd. So it's the answer.
In addition, nice post, @Shuaishuai
Looks like the general name of this problem is "Chinese postman's problem" - "finding the minimum length, edge-covering tour of a graph G(N, A) with no restrictions placed on G other than that it be connected and undirected." http://web.mit.edu/urban_or_book/www/book/chapter6/6.4.4.html
Nice abstract, but this problem seems easier than Chinese postman's problem, because the length of every edges are equal.
this is a cool reduction of the problem... thanks guys :D
Your analysis is splendid. But I just have some troble understanding why we could transform the problem into the one relating to Eular path and semi-Eulerian graph. Could you explain it to me? Thank you!
Since each pair of (x, y) is connected, I came to the thought of a complete graph. Also, considering that a[1]-a[2]-a[3]-...-a[n] is a road that goes through all the edges in the graph, I determined that this graph is semi-Eulerian.
Here is an easier way to code the same: 45590224
THERE ARE TWO CASES 1) NUMBER OF VERTICES ARE ODD THEN IN THE COMPLETE GRAPH THE DEGREE OF EVERY VERTEX WOULD BE EVEN AND THIS IS A NECESSARY AND SUFFICIENT CONDITION FOR A EULER GRAPH AS ALL THE VERTICES HAVE EVEN DEGREE AND THERE IS ONLY ONE COMPONENT IN THE GRAPH AND IT CONTAINS ALL THE EDGES SO EULER TOUR IS POSSIBLE IN THIS GRAPH IN THIS WAY WE CAN TRAVEL THROUGH EACH OF THE N*(N-1)/2 EDGES EXACTLY ONCE AND IT IS A EULER TOUR OF THE GRAPH.2)NUMBER OF VERTICES ARE EVEN THEN IN THE COMPLETE GRAPH THE DEGREE OF EVERY VERTEX WOULD BE ODD AND THIS IS NOT SUFFICIENT CONDITION FOR A EULER OR A SEMI EULERIAN GRAPH BUT WE CAN MAKE IT A SEMI EULERIAN GRAPH BY MAKING THE DEGREE OF N-2 VERTICES AND EVEN AND LEAVING THE OTHER TWO AS ODD IN THIS WAY WE CAN TRAVEL THROUGH EACH OF THE EDGES (N*(N-1))/2 ATLEAST ONCE AND THAT TOO IN MINIMUM NUMBER OF STEPS AND IT IS THE SEMI EULERIAN TOUR OF THE GRAPH.