Binary search is a very familiar algorithm to most people here. A typical implementation looks like this:
// x = array of numbers
// n = length of the array
// k = search key
// returns "true" if the key is found, "false" otherwise
bool search(int x[], int n, int k) {
int l = 0, r = n-1;
while (l <= r) {
int m = (l+r)/2;
if (x[m] == k) return true;
if (x[m] < k) l = m+1; else r = m-1;
}
return false;
}
However, even if the idea is straightforward, there are often bugs in binary search implementations. How exactly to update the search bounds and what is the condition when the search should stop?
Here is an alternative binary search implementation that is shorter and should be easier to get correct:
bool search(int x[], int n, int k) {
int p = 0;
for (int a = n; a >= 1; a /= 2) {
while (p+a < n && x[p+a] <= k) p += a;
}
return x[p] == k;
}
The idea is to implement binary search like linear search but with larger steps. Variable p contains the current array index, and variable a contains the step length. During the search, the step length is n, n/2, n/4, ..., 1. Finally, p contains the largest index whose value is not larger than the search key.
A similar idea can be applied to binary search variations. For example, the following code counts how many times the key appears in the array. After the search, [p+1..q] is the range with value k.
int count(int x[], int n, int k) {
int p = -1, q = -1;
for (int a = n; a >= 1; a /= 2) {
while (p+a < n && x[p+a] < k) p += a;
while (q+a < n && x[q+a] <= k) q += a;
}
return q-p;
}
Do you know other tips how to implement binary search correctly?











thanks for the second implementation it was a new and of course tricky implementation to me.:D
Well, imagine you an array [0..n - 1] and let us have an invariant: some function F which returns True for every a[i] as an argument for any i from [0..k] and False for every a[j] for j from [k + 1..n - 1]. Then my binary search which actually finds the border between these two parts of the array looks the following way:
You can easily prove that l = k and r = k + 1 by the end of the while loop. In this case no worries about whether to increase m by 1 or not.
As an example this is the code which determines whether an element x exists in the sorted array [0..n-1]:
http://codeforces.com/contest/812/problem/C I got many bugs earlier , but with your implementation , AC in one go :)
BTW , do you always use this implementation , or adapt different version like h = mid + 1 etc , sometimes?
Hi I'm always use this binary search, you never need use r = mid + 1, but here are 2 tricks:
1) To select the l, and r values you need:
For l take a value that can never happen for left. (foribidden value left)
For r take a value that can never happen for right. (forbidden value right)
For example in an array we never can access to index -1, or the index N (assuming 0 to N-1 indexing) then l = -1, r = n
Or on this problem: http://codeforces.com/gym/101908/problem/G
(solution) https://pastebin.com/jqe0Zh5T
First read the problem. A problem about binary search on a flow I pick 0 for left value, because I know that is impossible fill all stations in 0 minutes. and I picked 1000001 for right value, because I know that is unnecessary using more time of the max time (1000000 limit of T in Tthe problem) to travel from a point A to point B. (also I can use right = max(T[i], for i from 0 to n -1) + 1.
So if your binary search ends and the value of b is the forbidden value means that no element meets the property.
2) Nerver use this binary search for doubles, obviously u can code something like this:
But this implementation is prone to errors of precision, more than once it has happened to me.
On the week 2 of: https://courses.edx.org/courses/course-v1:ITMOx+I2CPx+3T2016/course/ explains about the reason it gives problems with doubles. When u need find some propertie on doubles u can use:
P.s I know the question was from months ago, but I hope someone finds it useful now.
Stumbling upon this implementation seven years later, yet the simplicity of this is amazing! Thanks!
Thanks Man !!! Nice way to implement
As a suggestion, As we all know that Binary Search runs in O(logn) so implementing it recursive will not only be that bad in case of running time or memory, but also it can decrease the number of bugs you might have :)
And one other bug that anyone could have is stop condition of binary search. As a suggestion you can have a condition that when r-l<=2 check remaining items yourself. It can also decrease the number of bugs you might have.
And as the final word, bounds are very important in implementing binary search. Searching for the first occurrence, last one, or the one after last one,or etc. will require different bounds of passing middle point and left or right to the function.
Here is an example usage of Binary Search for Problem C,Round 218 : 5384392
P.S. Sorry for my bad english :)
Usually, when I have doubts about errors implementing binary search, which are common when I have to find things like "the largest element with this and that conditions..." (also lower_bound, upper_bound, etc), I do the following. I make the main loop of the binary search like this:
while (hi-lo > 5) { // here the usual binary search code }
and then, after that, a small linear loop for getting the correct result.
while (lo != hi) // increment or decrement hi or lo, respectively
The number 5 has nothing of special. It only ensures that the remaining interval is small enough. This avoids the possibility of errors on termination of the main loop of binary search, or the wrong choose of lo or hi. Although this approach is nice for saving you during a contest, it is not that good for understanding and proving correctness, which is fair more valuable IMHO.
I hope it was useful.
Let me try to generalize nhtrnm's answer a bit:
So far, every single time I used (integer) binary search, I could formulate the problem in one of two ways:
(1) Given a range of integers R = {l, l + 1, ..., r - 1, r} and a monotonically increasing predicate P, find the smallest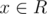 for which P(x) holds true. I then use the following code:
for which P(x) holds true. I then use the following code:
This might not work if P(r) = 0 (in this case the algorithm will return x = r), but you can easily extend your search range to
r + 1and artificially set P(r + 1) = 1 or you can just precheck for that situation.(2) Given a range of integers R = {l, l + 1, ..., r - 1, r} and a monotonically decreasing predicate P, find the largest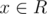 for which P(x) holds true. If we set Q(x) = !P(x), then Q is increasing and we can use (1) to find x + 1. We can also just use the following slightly modified variant:
for which P(x) holds true. If we set Q(x) = !P(x), then Q is increasing and we can use (1) to find x + 1. We can also just use the following slightly modified variant:
I find this approach so intuitive that I haven't done a single mistake while implementing binary search since.
In the case of finding the occurence of an element k in a sorted array, I would use variant (1) to find the first element
i >= kand then check whetheri = k. Note that in the case where k > x[n - 1] the algorithm still works because of the equality check at the end.So, to summarize, you don't need to use this particular method, but you should have realized that there is really only one type of problem that can be solved with binary search and stick to only one particular implementation to solve this problem. You won't make a single mistake with binary search from there on.
what is x in "if" condition, because search value is k??
Sorry, fixed
i found a good binary search problem. and in my experience when you wanna minimize the maximum of something or maximize the minimum of something binary search is a good idea.
I lost track of how many problems I couldn't solve because of bad binary search implementations. Even this year during IOI I couldn't manage to solve completely one of the problems because my binary search had a bug that I wasn't able to find :(
if an array contains the following data: 1 2 3 4 4 4 4 4 4 6 7 8 Now I want to find the position of first occurance of data 4. How can I implement binary search for this problem? Here, the answer should be 3.
Something like this:
This guarantees that you won't miss the earliest occurrence of 4, since whenever you see a 4, it's the right bound that is modified, not the left bound.
Generalized implementation of lower bound for non-decreasing func :
Actually you don't need
whilein your second implementation. You can use justif, can't you?while is needed, because the steps are not always powers of 2.
while is needed, because the steps are not always powers of 2. ****If not ,Then please let me learn how the run time could be log2(n)???
This is just a handwave-y explanation I thought of on the spot, so it's probably not 100% accurate, but this should at least give you a basic idea.
So in the first place, we would've already determined that the loop condition at a step size of $$$n$$$ is false in order to go into the next iteration of the for loop with size $$$\lfloor \frac{n}{2} \rfloor$$$.
It is clear that $$$3 \times \lfloor \frac{n}{2} \rfloor \geq n$$$ so the while loop will run at most twice since it will always break at the third iteration as the loop condition will always return false. We can assume that the inner loop will execute at most $$$3$$$ comparisons.
It is also clear that the outer loop will run at most $$$log(n)$$$ times since it divides by $$$2$$$ each time, therefore this implementation will overall take at most $$$log(n) \times 3$$$ operations which is $$$O(log(n))$$$ since $$$3$$$ is a constant.
To be clear on why the while statement is needed, you can try finding $$$5$$$ in $$$[1, 2, 3, 4, 5]$$$ with an if statement in place of the while statement.
This Code Work Perfectly::
int main(){
IOS;
int t; cin >> t;
while(t--){
int n, target; cin >> n >> target; vctr v(n); Trav(x, v) cin >> x; SRT(v); if(v[n-1] < target || v[0] > target) cout <<target<< " is Out of Range\n"; else{ int pos = 0; for(int a = n-1; a > 0; a/=2){ //while(pos+a < n and v[pos+a] <= target) pos+=a; if(pos+a < n and v[pos+a] <= target) pos+=a; } if(v[pos]==target) cout << target <<" is present in the array at index "<<pos+1<<"\n"; else cout <<"Opps! "<< target <<" is not found in the array\n"; }}
return 0;
}
Input::
4
5 5
1 2 3 4 5
5 4
1 2 3 4 5
5 1
1 2 3 4 5
5 100
1 2 3 4 5
Output::
5 is present in the array at index 5
4 is present in the array at index 4
1 is present in the array at index 1
100 is Out of Range
===== Used: 0 ms, 4 KB
That works for this specific case because you're starting with a jump size of $$$N - 1$$$, which in this case is $$$4$$$, i.e. a power of $$$2$$$. This doesn't work in other cases where $$$N - 1$$$ doesn't give you a power of $$$2$$$.
If you really want to avoid using a while loop, someone below has suggested using $$$2^{ \lfloor log2(n) \rfloor }$$$ as the starting jump size, but I think that would be slower than just using a while since you'd need to compute that first by calling
1 << (int) log2(n)first, unless $$$n$$$ is constant and the compiler optimizes that out. This method does give the minimum amount of queries possible though, which may be useful e.g. in interactive problems.Anyway, just use a while loop if you really do want to use this specific implementation. Both implementations work just fine though. My ICPC teammates often go with the regular
while(l < r)implementation while I usually use thefor(int i = n; i > 0; i /= 2)implementation. We've never had TLEs because of either implementation, so it's pretty much just a matter of which way you prefer.Thank you bro...
actually I used a = n-1 for the array bound, but I didn't thought it that if (n-1) isn't a power of 2 then using ( if ) statement instead of ( while ) will give an error....
Thank you again for giving your time...
Glad to help. Have fun coding!
I used to write binary search like this:
I think this is more like Exponential search. It always performs at least as efficient as binary search.
This is simply awesome !
bool search(int x[], int n, int k) { int p = 0; for (int a = n; a >= 1; a /= 2) { while (p+a < n && x[p+a] <= k) p += a; } return x[p] == k; }
@pllk why do we need p=-1 in the count function while in search implementation p starts with 0.
I think we do not need, i.e. the code with p=0, q=0 also works.
In the second approach , It is more efficient if we take initial jump as a = n/ 2 instead a = n .
If n == 1 then the it can give wrong ans in some situation.
Great post, this will change the way I implement binary search in the future. Sometimes (interactive problems with limited number of queries) we want to use the minimum number of queries possible, and I thinking modify your code to do that gives an even prettier implementation, since it also gets rid of the inner while loop. Just fix one bit at a time starting from the leading bit of n (namely, $$$2^{\lfloor log2(n)\rfloor}$$$):