And while everyone is relaxing after TopCoder, I would like to remind that today at 21:00 UTC the Round 2 of Facebook Hacker Cup 2014 is taking place. It will run for 3 hours. Top 100 advance to Round 3 and get a T-shirt.
→ Pay attention
→ Streams
→ Top rated
| # | User | Rating |
|---|---|---|
| 1 | ecnerwala | 3648 |
| 2 | Benq | 3580 |
| 3 | orzdevinwang | 3570 |
| 4 | cnnfls_csy | 3569 |
| 5 | Geothermal | 3568 |
| 6 | tourist | 3565 |
| 7 | maroonrk | 3530 |
| 8 | Radewoosh | 3520 |
| 9 | Um_nik | 3481 |
| 10 | jiangly | 3467 |
→ Top contributors
| # | User | Contrib. |
|---|---|---|
| 1 | maomao90 | 174 |
| 2 | adamant | 164 |
| 2 | awoo | 164 |
| 4 | TheScrasse | 160 |
| 5 | nor | 159 |
| 6 | maroonrk | 156 |
| 7 | -is-this-fft- | 150 |
| 8 | SecondThread | 148 |
| 9 | pajenegod | 145 |
| 9 | orz | 145 |
→ Find user
→ Recent actions
↑
↓
Codeforces (c) Copyright 2010-2024 Mike Mirzayanov
The only programming contests Web 2.0 platform
Server time: Apr/18/2024 04:11:27 (i1).
Desktop version, switch to mobile version.
Supported by
User lists


| Name |
|---|











The contest will be available here.
All those who could not qualify for this round (like me)can view leader board here !
My thoughts about the problems:
WAT? 3 times combinatorics? It's too narrow, even if all 3 problems could be solved in different ways...
Hm, the results are out. WAT? again, I flew up 100 places and got to round 3... submitting 5 minutes before the end, like a boss :D
Problem 1 was suitably easy, just two pointers using set<>s to store the sets of colours was sufficient.
Problem 3 was also suitably hard, requiring the right idea, and an efficient, although not difficult, implementation.
I managed to finalize this idea about 30 minutes before the end: Every vertex i gives us the number of ways Pi to choose slopes leading to it directly, and it's only dependent on the first i numbers of the input (denote those as Ai). To find it, we construct a tree where vertex j is the son of vertex Aj. If we add a direct slope from j < i to i, every path containing that slope will be passing through every vertex on the path from the root (vertex 0) to j, and there will be some path not passing through any vertex not on that path and < i, so Ai must be on that path, or equivalently, we can only add direct slopes to i from children of Ai in that tree. By the same idea, we find out that those direct slopes can't all be from the subtree of one of the sons of Ai; if those sons have subtree sizes S1..k, then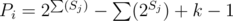 . All that's left is constructing the tree, counting
. All that's left is constructing the tree, counting  by one DFS and counting Pi, all in O(N), giving us O(N2) total complexity. I wonder if it could be solved more efficiently...
by one DFS and counting Pi, all in O(N), giving us O(N2) total complexity. I wonder if it could be solved more efficiently...
I didn't like problem 2, though. I couldn't escape a lot of casework by inclusion/exclusion... is there any nice way to solve it?
Problem 3 is solvable in O(N log2 N) time (UPD: WRONG). All that we need is to keep track of sizes of subtrees. Let build an heavy light decomposition on the whole tree (with all N vertices). Then after processing vertex i, we will add it to the tree. Adding vertex is equivalent to increasing by one all sizes on the path from the root to this vertex.
Of course, for this problem it is an overkill and during the competition I've implemented O(N2) one :)
In the worst case you need to get sizes of subtrees O(N2) times (for example when Ai = 0 for all i).
O(N5) brute force worked in Problem 2...
Ok, you are right. But, if I'm not wrong again (at least now is not 3 AM), there is an solution.
solution.
Let construct the whole tree and divide there all vertices into two sets: big and small vertices. Big vertices will be all vertices with size of subtree (in the whole tree) greater than , small will be all other vertices. Also, like in the first (slow) solution, let build an heavy light decomposition on the whole tree.
, small will be all other vertices. Also, like in the first (slow) solution, let build an heavy light decomposition on the whole tree.
Now, we will again add to the tree vertices one by one, but we will keep track of two values:
SV — size of subtree in current tree and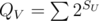 , where U is looping through all small sons of vertex V.
, where U is looping through all small sons of vertex V.
Now, how we will add a vertex: I can't explain it clearly in words, so the pseudocode:
I hope it's clear, that while loop will iterate at most times per vertex, so adding one vertex takes
times per vertex, so adding one vertex takes  time.
time.
Now, how to calculate PV (from Xellos comment):
So, the overall complexity of this solution is .
.
You can solve Problem 2 with dynamic programming in O(n). You can count the remaining three pairs from those with higher maximum numbers towards lower. Let's say that pair (x, y), x < y will be the largest. If you fix y, you can choose x from somewhere in the range 1..x'. When you'll have to choose the next pair (a, b), b<y, you know that the range of possible values for a will be 1..a', x' ≤ a'. Therefore, it doesn't matter which x was chosen in the previous step, only how many pairs were chosen before.
In fact you're solving a generalized problem f(k, n) of choosing k pairs from numbers 1..n such that their sum is at most c1 + c2. Time complexity is just O(kn). You either use n as a part of the largest pair or not. There are a couple of things to consider, like how to handle used values c1, c2 and make sure that x < y, but it can be done.
Pretty nice approach,thanks for sharing