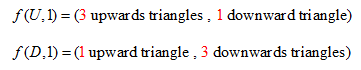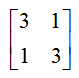The second problem that made its way here is “Trace”, both because it was an interesting problem on its own right and also because I really like Sherlock Holmes’ books.
- Understanding the problem statement
Apart from having an exciting background story, there is some information we need to take note of if we are to solve this problem correctly:
“ (…) the red and the blue color were alternating, i. e. followed one after the other. The outer area of the wall (the area that lied outside all circles) was painted blue. (…)”
“Let us remind you that two circles are called concentric if their centers coincide. Several circles are called concentric if any two of them are concentric.”
Those two sentences above are the key in solving this problem.
From the first one, we can immediately tell, that the circle with larger radius will be red, and the others will be: blue, red, blue, red, etc, accordingly to the pattern described above. The second sentence, describes to us the definition of concentric circles, and from there we can tell that all circles should be centered on the same arbitrarily chosen origin, in order to respect the constrain of being concentric (we shall choose point (0, 0) on a standard xOy Cartesian plane as the origin). Having the initial setup of the problem cleared out, we shall start thinking on a solution.
- Understanding given test cases
On all programming problems, contestants are given some sample input tests, which are there to make sure the reader fully understands the problem statement and can work out some easy cases by hand. However, they play a much larger role as we will see ahead. The first test case given is trivial, we have only one circle whose radius is 1, so, the portion of the wall which should be painted red is the part taken by the whole circle, so the answer is:
3.141592653589793
This also tells us the precision of the constant pi used by the online judge, and it will suffice to use such precision on our code (so, ultimately, even the simplest test case can provide itself of use).
The second test case is a bit more complex than the previous one, but it’s still possible to work through it by hand. Let’s see what arises as new information to us from it:
We now have three circles of radii 1,4,2 respectively. However, if we follow the convention adopted on the beginning of this editorial, i.e., representing all circles on the same origin point, we see that the order on which they are given on the input it’s not important and that the outer circle (circle with larger radius) will always be painted red, as the plane is painted blue. So, it comes naturally, that this is actually a sorting problem, mixed with some geometry (after all, we have circles involved :p).
- Building a solution and spotting a really tricky test case
So, now all we have to do is sort the given circles in ascending order, and start iterating from the outer to the inner circle, as we know the outer one will be red.
Assume now we have a vector, conveniently called radii, ordered like:
radii = [1,2,3…N];
Circle N will be located at index radii.size() – 1 and it will be red, so we need to account for it on our calculations for the red covered area. The next circle will be located at index radii.size()-2 and we will subtract it from our current answer (as we englobed the area of all circles before), then we will sum the one at index radii.size()-3 and so on…
So, as the circle on index 0 will always be red, if index%2 == 0 we sum that area to our answer, if not, we subtract it, and our solution is built…
Almost…
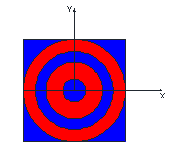
There can be the case of when the blue area is larger than the red area, case where the result will be correct, but with the sign reversed, so, on that case, if answer is < 0, we output ans*(-1).
This is the case of system test #3, which caught me off guard for such fact, so, considering all scenarios is critical to achieve sucess.
(Reference:
System test #3:
4
4 1 3 2 )
Figure below attempts to illustrate such case and also illustrates what was described during the analysis.
- Code and final remarks
The code itself is straightforward after we follow this analysis on a step by step fashion. The only remark that seems adequate to do is that it's safer to use double data type instead of float, as float would lose precision and yield wrong answer if required precision was 10e-6.

Once again, hope you liked it and suggestions and feedback is very valuable to me as a writer, so thanks for reading!!
Best regards,
Bruno