In this problem one need to determine the number of points for both guys and find out who got more points.
Time complexity: O(1).
501B - Misha and Changing Handles
The problem can be formulated as follows: The directed graph is given, its vertices correspond to users' handles and edges — to requests. It consists of a number of chains, so every vertex ingoing and outgoing degree doesn't exceed one. One need to find number of chains and first and last vertices of every chain. The arcs of this graph can be stored in dictionary(one can use std::map\unoredered_map in C++ and TreeMap\HashMap in Java) with head of the arc as the key and the tail as the value.
Each zero ingoing degree vertex corresponds to unique user as well as first vertex of some chain. We should iterate from such vertices through the arcs while it's possible. Thus we find relation between first and last vertices in the chain as well as relation between the original and the new handle of some user.
You can see my solution for details.
Time complexity: 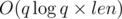 .
.
Note that every non-empty forest has a leaf(vertex of degree 1). Let's remove edges one by one and maintain actual values (degreev, sv) as long as graph is not empty. To do so, we can maintain the queue(or stack) of the leaves. On every iteration we dequeue vertex v and remove edge (v, sv) and update values for vertex sv: degreesv -= 1 and ssv ^= v. If degree of vertex sv becomes equal to 1, we enqueue it.
When dequeued vertex has zero degree, just ignore it because we have already removed all edges of corresponding tree.
You can see my solution for details.
Time complexity: O(n)
504B - Misha and Permutations Summation
To solve the problem, one need to be able to find the index of given permutation in lexicographical order and permutation by its index. We will store indices in factorial number system. Thus number x is represented as 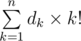 . You can find the rules of the transform here.
. You can find the rules of the transform here.
To make the transform, you may need to use data structures such as binary search tree or binary indexed tree (for maintaining queries of finding k-th number in the set and finding the amount of numbers less than given one).
So, one need to get indices of the permutations, to sum them modulo n! and make inverse transform. You can read any accepted solution for better understanding.
Time complexity:  or
or  .
.
504C - Misha and Palindrome Degree
Note that if the amount of elements, which number of occurrences is odd, is greater than one, the answer is zero. On the other hand, if array is the palindrome, answer is 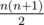 .
.
Let's cut equal elements from the end and the beginning of array while it is possible. Let's call remaining array as b and its length as m. We are interested in segments [l, r] which cover some prefix or suffix of b.
We need to find the minimum length of such prefix and suffix. Prefix and suffix can overlap the middle of b and these cases are needed to maintain. To find minimum length you can use binary search or simply iterating over array and storing the amount of every element to the left and right from the current index. Let's call minimum length of prefix as pref and as suf of suffix. So 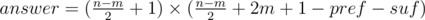 .
.
Time complexity: O(n) or  .
.
Firstly, we convert each number into a binary system: it can be done in O(MAXBITS2), where MAXBITS ≤ 2000 with rather small constant(we store number in system with big radix).
To solve the problem we need to modify Gauss elimination algorithm. For each row we should store set of row's indices which we already XORed this row to get row echelon form (we can store it in bitset), also for each bit i we store index p[i] of row, which lowest set bit is i in row echelon form.
Maintaining the query we try to reset bits from lowest to highest using array p and save information, which rows were XORed with current number. If we can reset whole number, the answer is positive and we know indices of answer. We update array p, otherwise.
Time complexity: O(m × MAXBITS × (MAXBITS + m)) with small constant due to bit compression.
Let's build heavy-light decomposition of given tree and write all strings corresponding to heavy paths one by one in one string T, every path should be written twice: in the direct and reverse order.
Maintaining query we can split paths (a, b) и (c, d) into parts, which completely belongs to some heavy paths. There can be at most  such parts. Note that every part corresponds to some substring of T.
such parts. Note that every part corresponds to some substring of T.
Now we only need to find longest common prefix of two substrings in string T. It can be done building suffix array of string T and lcp array. So, we can find longest common prefix of two substring in O(1) constructing rmq sparse table on lcp array.
Time complexity: 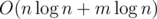
For the better understanding see my solution.
P.S. One can uses hashes instead of suffix array.
ADD: There is another approach to solve this problem in 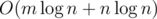 but it's rather slow in practice. We can do binary search on answer and use hashes, but we do it for all queries at one time. The only problem is to find k-th vertex on the path, we can do it offline for all queries in O(n + m) time. We run dfs and maintain stack of vertices. See my solution for details.
but it's rather slow in practice. We can do binary search on answer and use hashes, but we do it for all queries at one time. The only problem is to find k-th vertex on the path, we can do it offline for all queries in O(n + m) time. We run dfs and maintain stack of vertices. See my solution for details.








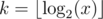 . And someone can see that
. And someone can see that  times, it can be calculated in a loop
times, it can be calculated in a loop 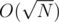 . And I'm interested in technical realization of it. Can anybody show how to write accurate brute-force or factorization for example on C/C++? And what advices can you give to write same programs, making as less operations as possible? It's the problem from acm.timus.ru
. And I'm interested in technical realization of it. Can anybody show how to write accurate brute-force or factorization for example on C/C++? And what advices can you give to write same programs, making as less operations as possible? It's the problem from acm.timus.ru 

