I'd like to invite everybody to participate in HourRank 12 on HackerRank. It'll start tomorrow at 19:30 PM MSK.
It's my first HourRank but I've prepared problems for HackerRank several times. I also used to prepare problems for Codeforces long time ago.
There will be three problems and one hour to solve them. Contest will be rated and top-10 contestants on the leaderboard will receive amazing HackerRank T-shirts!
I'd like to thank wanbo for testing the problems, it's always a pleasure to work with him. I hope you will enjoy the problems and some of you will solve everything.
Scoring will be: 20-40-80. Editorials will be published right after the contest.
Good luck!









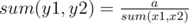 . Не стоит забывать про случай
. Не стоит забывать про случай 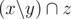 . Теперь осталось найти кратчайшую последовательность множеств
. Теперь осталось найти кратчайшую последовательность множеств 
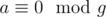 где
где 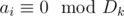 для любого
для любого 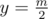 в декартовой системе координат.
в декартовой системе координат.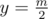 , перебрать все отрезки
, перебрать все отрезки 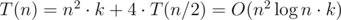 для квадратных досок. Для прямоугольных это сумма соответствующих выражений для
для квадратных досок. Для прямоугольных это сумма соответствующих выражений для 
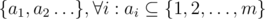 и не существует
и не существует 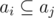 .
.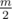 элементов. Но доказать это у меня не получилось. Где можно почитать об этом?
элементов. Но доказать это у меня не получилось. Где можно почитать об этом?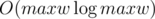 . Мне интересно, это боян?
. Мне интересно, это боян? 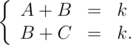
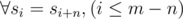
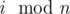 . Для всех
. Для всех 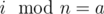 .
.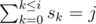 .
. 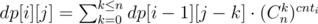
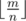 и
и 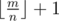 . Посчитаем
. Посчитаем 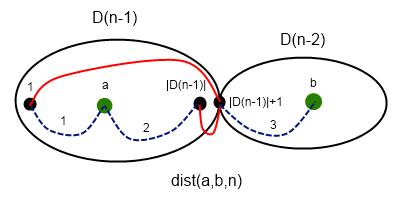
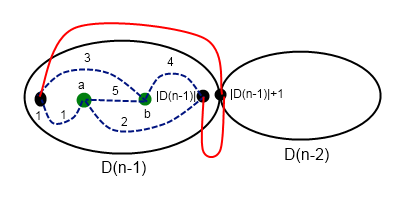
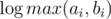 на запрос (логарифм возникает из соображения о том, что размеры графов в зависимости от порядка растут экспоненциально). Важно было запускать алгоритм не для данного
на запрос (логарифм возникает из соображения о том, что размеры графов в зависимости от порядка растут экспоненциально). Важно было запускать алгоритм не для данного 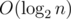 или за
или за 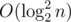 .
. 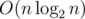 , запрос
, запрос 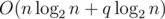 . Однако решения, выполняющие запрос
. Однако решения, выполняющие запрос 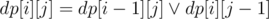 для правой половины доски.
для правой половины доски. 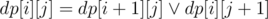 (
(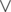 — логическое или, в данном случае имеется в виду побитовое или для масок) для левой. Динамика считаем маску доступных клеток на центральном столбце.
— логическое или, в данном случае имеется в виду побитовое или для масок) для левой. Динамика считаем маску доступных клеток на центральном столбце.
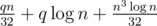 .
. 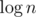 битсетов — множеств доступных клеток на столбцах, выбираемых центральными.
битсетов — множеств доступных клеток на столбцах, выбираемых центральными.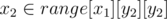 и верно
и верно 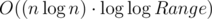 (
(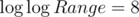 и я не уверен
и я не уверен 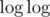 ли это). Идея тупая: каждое число станет единицей, если взять корень
ли это). Идея тупая: каждое число станет единицей, если взять корень 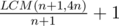 крестиков.
крестиков. подряд, то они ничего не изменили и их можно переместить в любое место нашего алгоритма, не изменив его результат. Тогда можно перебирать только те алгоритмы, в которых все парные операции
подряд, то они ничего не изменили и их можно переместить в любое место нашего алгоритма, не изменив его результат. Тогда можно перебирать только те алгоритмы, в которых все парные операции 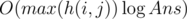 , если решать задачу в рациональных числах.
, если решать задачу в рациональных числах.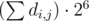 . Таким образом, можно решать задачу в рациональных числах или в типе double.
. Таким образом, можно решать задачу в рациональных числах или в типе double.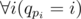 , то мы получим ответ для исходной задачи и перестановки.
, то мы получим ответ для исходной задачи и перестановки.
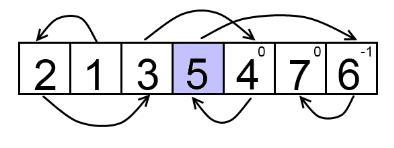
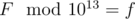 . (
. (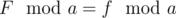 ).
).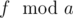 в период последовательности Фибоначчи по модулю
в период последовательности Фибоначчи по модулю 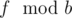 в период последовательности Фибоначчи по модулю
в период последовательности Фибоначчи по модулю 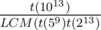 чисел.
чисел.
