| Codeforces Global Round 4 |
|---|
| Finished |
Every person likes prime numbers. Alice is a person, thus she also shares the love for them. Bob wanted to give her an affectionate gift but couldn't think of anything inventive. Hence, he will be giving her a graph. How original, Bob! Alice will surely be thrilled!
When building the graph, he needs four conditions to be satisfied:
- It must be a simple undirected graph, i.e. without multiple (parallel) edges and self-loops.
- The number of vertices must be exactly $$$n$$$ — a number he selected. This number is not necessarily prime.
- The total number of edges must be prime.
- The degree (i.e. the number of edges connected to the vertex) of each vertex must be prime.
Below is an example for $$$n = 4$$$. The first graph (left one) is invalid as the degree of vertex $$$2$$$ (and $$$4$$$) equals to $$$1$$$, which is not prime. The second graph (middle one) is invalid as the total number of edges is $$$4$$$, which is not a prime number. The third graph (right one) is a valid answer for $$$n = 4$$$.
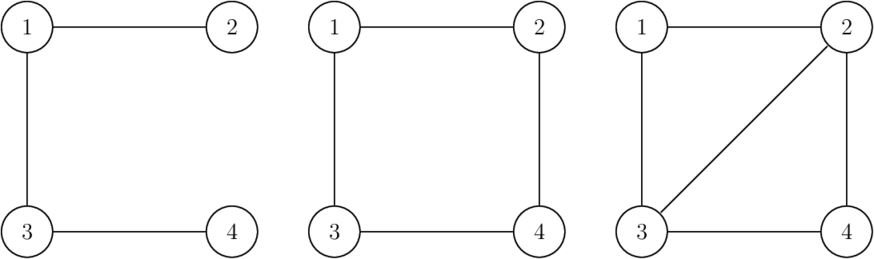
Note that the graph can be disconnected.
Please help Bob to find any such graph!
The input consists of a single integer $$$n$$$ ($$$3 \leq n \leq 1\,000$$$) — the number of vertices.
If there is no graph satisfying the conditions, print a single line containing the integer $$$-1$$$.
Otherwise, first print a line containing a prime number $$$m$$$ ($$$2 \leq m \leq \frac{n(n-1)}{2}$$$) — the number of edges in the graph. Then, print $$$m$$$ lines, the $$$i$$$-th of which containing two integers $$$u_i$$$, $$$v_i$$$ ($$$1 \leq u_i, v_i \leq n$$$) — meaning that there is an edge between vertices $$$u_i$$$ and $$$v_i$$$. The degree of each vertex must be prime. There must be no multiple (parallel) edges or self-loops.
If there are multiple solutions, you may print any of them.
Note that the graph can be disconnected.
4
5 1 2 1 3 2 3 2 4 3 4
8
13 1 2 1 3 2 3 1 4 2 4 1 5 2 5 1 6 2 6 1 7 1 8 5 8 7 8
The first example was described in the statement.
In the second example, the degrees of vertices are $$$[7, 5, 2, 2, 3, 2, 2, 3]$$$. Each of these numbers is prime. Additionally, the number of edges, $$$13$$$, is also a prime number, hence both conditions are satisfied.

| Name |
|---|




