Изменения рейтингов за последние раунды временно удалены. Скоро они будут возвращены. ×

C. Анна, Святослав и карта
ограничение по времени на тест
2 секунды
ограничение по памяти на тест
256 мегабайт
ввод
стандартный ввод
вывод
стандартный вывод

Главные герои были опущены для краткости.

Вам дан ориентированный невзвешенный граф без петель с $$$n$$$ вершинами и путь в нём (не обязательно простой), заданный последовательностью $$$p_1, p_2, \ldots, p_m$$$ из $$$m$$$ вершин; для любого $$$1 \leq i < m$$$ существует дуга из $$$p_i$$$ в $$$p_{i+1}$$$.

Будем называть последовательность $$$v_1, v_2, \ldots, v_k$$$ из $$$k$$$ вершин хорошей, если $$$v$$$ является подпоследовательностью $$$p$$$, $$$v_1 = p_1$$$, $$$v_k = p_m$$$, и $$$p$$$ является одним из кратчайших путей, проходящих через вершины $$$v_1$$$, $$$\ldots$$$, $$$v_k$$$ в этом порядке.

Последовательность $$$a$$$ является подпоследовательностью $$$b$$$, если $$$a$$$ может быть получена из $$$b$$$ удалением нескольких (возможно, ни одного или всех) элементов. Очевидно, что последовательность $$$p$$$ является хорошей, но вам предстоит найти кратчайшую хорошую подпоследовательность.

Если существует несколько кратчайших хороших подпоследовательностей, выведите любую.

Входные данные

Первая строка содержит одно целое число $$$n$$$ ($$$2 \le n \le 100$$$) — количество вершин в графе.

Следующие $$$n$$$ строк задают граф матрицей смежности: $$$j$$$-й символ в $$$i$$$-й строке равен $$$1$$$, если есть дуга из вершины $$$i$$$ в вершину $$$j$$$, иначе равен $$$0$$$. Гарантируется, что заданный граф не имеет петель.

Следующая строка содержит одно целое число $$$m$$$ ($$$2 \le m \le 10^6$$$) — количество вершин в выбранном пути.

Следующая строка содержит $$$m$$$ целых чисел $$$p_1, p_2, \ldots, p_m$$$ ($$$1 \le p_i \le n$$$) — вершины в пути. Гарантируется, что для любого $$$1 \leq i < m$$$ существует дуга из $$$p_i$$$ в $$$p_{i+1}$$$.

Выходные данные

В первой строке выведите одно число $$$k$$$ ($$$2 \leq k \leq m$$$) — длину кратчайшей хорошей подпоследовательности. Во второй строке выведите $$$k$$$ целых чисел $$$v_1$$$, $$$\ldots$$$, $$$v_k$$$ ($$$1 \leq v_i \leq n$$$) — вершины в подпоследовательности. Если существует несколько кратчайших хороших подпоследовательностей, выведите любую. Любые два последовательные числа должны быть различны.

Примеры
Входные данные
4
0110
0010
0001
1000
4
1 2 3 4
Выходные данные
3
1 2 4
Входные данные
4
0110
0010
1001
1000
20
1 2 3 4 1 2 3 4 1 2 3 4 1 2 3 4 1 2 3 4
Выходные данные
11
1 2 4 2 4 2 4 2 4 2 4
Входные данные
3
011
101
110
7
1 2 3 1 3 2 1
Выходные данные
7
1 2 3 1 3 2 1
Входные данные
4
0110
0001
0001
1000
3
1 2 4
Выходные данные
2
1 4
Примечание

На рисунке представлен граф для первого примера:

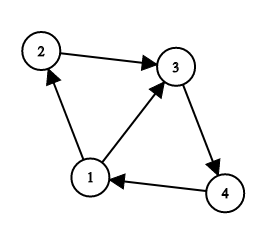
Заданный путь проходит через вершины $$$1$$$, $$$2$$$, $$$3$$$, $$$4$$$. Последовательность $$$1-2-4$$$ является хорошей, т.к. она является подпоследовательностью заданного пути, её первый и последний элементы совпадают с первым и последним элементом заданного пути, и кратчайший путь, проходящий через вершины $$$1$$$, $$$2$$$ и $$$4$$$ в этом порядке, это $$$1-2-3-4$$$. Обратите внимание, что последовательности $$$1-4$$$ и $$$1-3-4$$$ не подходят, т. к. в обоих случаях кратчайший путь, проходящий через вершины этих последовательностей, это $$$1-3-4$$$.

В третьем примере граф является полным, поэтому любая последовательность вершин, в которой любые два последовательных элемента различны, задаёт путь из такого же количества вершин.

В четвёртом примере пути $$$1-2-4$$$ и $$$1-3-4$$$ являются кратчайшими путями, проходящими через вершины $$$1$$$ и $$$4$$$.