Это упрощённая версия задачи. В этой версии, $$$n \le 6$$$.
Марек работает над тестами для новой задачи. Хотите узнать, для какой? Не-а, мы вам не скажем. Однако, мы скажем вам как он генерирует тесты.
Марек выбирает целое число $$$n$$$ и $$$n^2$$$ целых чисел $$$p_{ij}$$$ ($$$1 \le i \le n$$$, $$$1 \le j \le n$$$). Затем он генерирует случайный двудольный граф на $$$2n$$$ вершин. В этом графе есть $$$n$$$ вершин у левой доли: $$$\ell_1, \ell_2, \dots, \ell_n$$$, и $$$n$$$ вершин у правой доли: $$$r_1, r_2, \dots, r_n$$$. Для каждой пары $$$i$$$ и $$$j$$$, он добавляет в граф ребро между вершинами $$$\ell_i$$$ и $$$r_j$$$ с вероятностью $$$p_{ij}$$$ процентов.
Оказывается, что тест будет сильным, если в этом графе есть совершенное паросочетание. Какова вероятность, что это произойдет?
Можно показать, что ответ можно представить в виде $$$\frac{P}{Q}$$$, где $$$P$$$ и $$$Q$$$ взаимно простые целое число и $$$Q \not\equiv 0 \pmod{10^9+7}$$$. Обозначим за $$$Q^{-1}$$$ целое число, для которого верно $$$Q \cdot Q^{-1} \equiv 1 \pmod{10^9+7}$$$. Выведите значение $$$P \cdot Q^{-1}$$$ по модулю $$$10^9+7$$$.
В первой строке записано одно целое число $$$n$$$ ($$$\mathbf{1 \le n \le 6}$$$). Следующие $$$n$$$ строк описывают вероятности появления каждого ребра в графе. $$$i$$$-й из них содержит $$$n$$$ целых чисел $$$p_{i1}, p_{i2}, \dots, p_{in}$$$ ($$$0 \le p_{ij} \le 100$$$); $$$p_{ij}$$$ описывает вероятность, в процентах, наличия в графе ребра между вершинами $$$\ell_i$$$ и $$$r_j$$$.
Выведите одно целое число — вероятность, что в двудольном графе есть совершенное паросочетание, записанная как $$$P \cdot Q^{-1} \pmod{10^9+7}$$$ для $$$P$$$, $$$Q$$$ определенных ранее.
2 50 50 50 50
937500007
3 3 1 4 1 5 9 2 6 5
351284554
В первом примере, каждый из $$$16$$$ графов равновероятен. Из них у $$$7$$$ есть совершенное паросочетание:
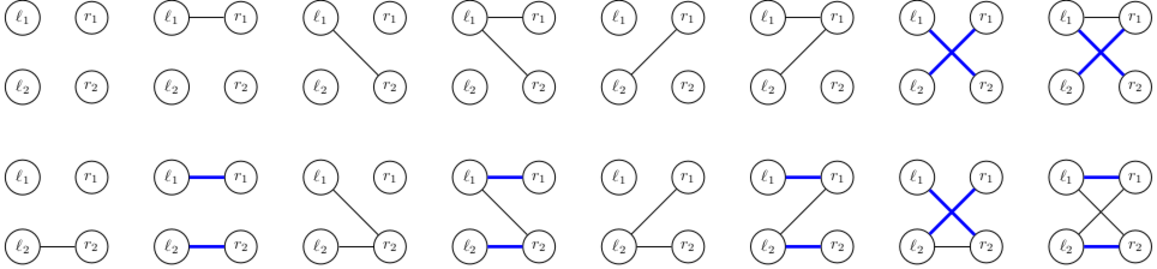
Таким образом, вероятность равна $$$\frac{7}{16}$$$. Так как $$$16 \cdot 562\,500\,004 = 1 \pmod{10^9+7}$$$, ответ на тест равен $$$7 \cdot 562\,500\,004 \mod{(10^9+7)} = 937\,500\,007$$$.
| Название |
|---|




