| Codeforces Global Round 5 |
|---|
| Finished |
This is a harder version of the problem. In this version, $$$n \le 50\,000$$$.
There are $$$n$$$ distinct points in three-dimensional space numbered from $$$1$$$ to $$$n$$$. The $$$i$$$-th point has coordinates $$$(x_i, y_i, z_i)$$$. The number of points $$$n$$$ is even.
You'd like to remove all $$$n$$$ points using a sequence of $$$\frac{n}{2}$$$ snaps. In one snap, you can remove any two points $$$a$$$ and $$$b$$$ that have not been removed yet and form a perfectly balanced pair. A pair of points $$$a$$$ and $$$b$$$ is perfectly balanced if no other point $$$c$$$ (that has not been removed yet) lies within the axis-aligned minimum bounding box of points $$$a$$$ and $$$b$$$.
Formally, point $$$c$$$ lies within the axis-aligned minimum bounding box of points $$$a$$$ and $$$b$$$ if and only if $$$\min(x_a, x_b) \le x_c \le \max(x_a, x_b)$$$, $$$\min(y_a, y_b) \le y_c \le \max(y_a, y_b)$$$, and $$$\min(z_a, z_b) \le z_c \le \max(z_a, z_b)$$$. Note that the bounding box might be degenerate.
Find a way to remove all points in $$$\frac{n}{2}$$$ snaps.
The first line contains a single integer $$$n$$$ ($$$2 \le n \le 50\,000$$$; $$$n$$$ is even), denoting the number of points.
Each of the next $$$n$$$ lines contains three integers $$$x_i$$$, $$$y_i$$$, $$$z_i$$$ ($$$-10^8 \le x_i, y_i, z_i \le 10^8$$$), denoting the coordinates of the $$$i$$$-th point.
No two points coincide.
Output $$$\frac{n}{2}$$$ pairs of integers $$$a_i, b_i$$$ ($$$1 \le a_i, b_i \le n$$$), denoting the indices of points removed on snap $$$i$$$. Every integer between $$$1$$$ and $$$n$$$, inclusive, must appear in your output exactly once.
We can show that it is always possible to remove all points. If there are many solutions, output any of them.
6 3 1 0 0 3 0 2 2 0 1 0 0 1 3 0 0 1 0
3 6 5 1 2 4
8 0 1 1 1 0 1 1 1 0 1 1 1 2 2 2 3 2 2 2 3 2 2 2 3
4 5 1 6 2 7 3 8
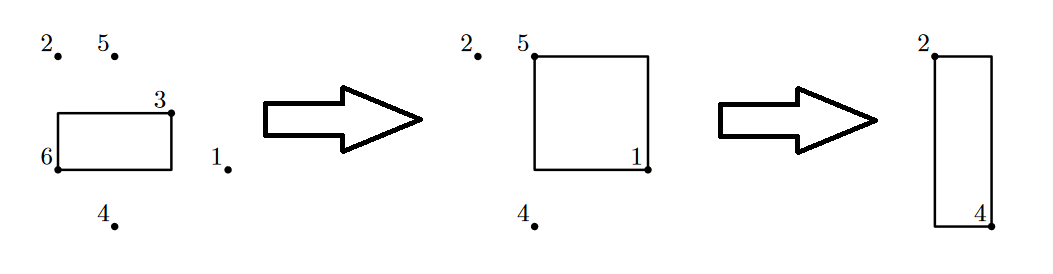
In the first example, here is what points and their corresponding bounding boxes look like (drawn in two dimensions for simplicity, as all points lie on $$$z = 0$$$ plane). Note that order of removing matters: for example, points $$$5$$$ and $$$1$$$ don't form a perfectly balanced pair initially, but they do after point $$$3$$$ is removed.
| Name |
|---|




