You are given a simple weighted connected undirected graph, consisting of $$$n$$$ vertices and $$$m$$$ edges.
A path in the graph of length $$$k$$$ is a sequence of $$$k+1$$$ vertices $$$v_1, v_2, \dots, v_{k+1}$$$ such that for each $$$i$$$ $$$(1 \le i \le k)$$$ the edge $$$(v_i, v_{i+1})$$$ is present in the graph. A path from some vertex $$$v$$$ also has vertex $$$v_1=v$$$. Note that edges and vertices are allowed to be included in the path multiple times.
The weight of the path is the total weight of edges in it.
For each $$$i$$$ from $$$1$$$ to $$$q$$$ consider a path from vertex $$$1$$$ of length $$$i$$$ of the maximum weight. What is the sum of weights of these $$$q$$$ paths?
Answer can be quite large, so print it modulo $$$10^9+7$$$.
The first line contains a three integers $$$n$$$, $$$m$$$, $$$q$$$ ($$$2 \le n \le 2000$$$; $$$n - 1 \le m \le 2000$$$; $$$m \le q \le 10^9$$$) — the number of vertices in the graph, the number of edges in the graph and the number of lengths that should be included in the answer.
Each of the next $$$m$$$ lines contains a description of an edge: three integers $$$v$$$, $$$u$$$, $$$w$$$ ($$$1 \le v, u \le n$$$; $$$1 \le w \le 10^6$$$) — two vertices $$$v$$$ and $$$u$$$ are connected by an undirected edge with weight $$$w$$$. The graph contains no loops and no multiple edges. It is guaranteed that the given edges form a connected graph.
Print a single integer — the sum of the weights of the paths from vertex $$$1$$$ of maximum weights of lengths $$$1, 2, \dots, q$$$ modulo $$$10^9+7$$$.
7 8 25 1 2 1 2 3 10 3 4 2 1 5 2 5 6 7 6 4 15 5 3 1 1 7 3
4361
2 1 5 1 2 4
60
15 15 23 13 10 12 11 14 12 2 15 5 4 10 8 10 2 4 10 7 5 3 10 1 5 6 11 1 13 8 9 15 4 4 2 9 11 15 1 11 12 14 10 8 12 3 6 11
3250
5 10 10000000 2 4 798 1 5 824 5 2 558 4 1 288 3 4 1890 3 1 134 2 3 1485 4 5 284 3 5 1025 1 2 649
768500592
Here is the graph for the first example:
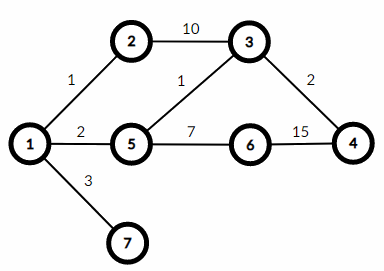
Some maximum weight paths are:
- length $$$1$$$: edges $$$(1, 7)$$$ — weight $$$3$$$;
- length $$$2$$$: edges $$$(1, 2), (2, 3)$$$ — weight $$$1+10=11$$$;
- length $$$3$$$: edges $$$(1, 5), (5, 6), (6, 4)$$$ — weight $$$2+7+15=24$$$;
- length $$$4$$$: edges $$$(1, 5), (5, 6), (6, 4), (6, 4)$$$ — weight $$$2+7+15+15=39$$$;
- $$$\dots$$$
So the answer is the sum of $$$25$$$ terms: $$$3+11+24+39+\dots$$$
In the second example the maximum weight paths have weights $$$4$$$, $$$8$$$, $$$12$$$, $$$16$$$ and $$$20$$$.
| Name |
|---|




