You are given four different integer points $$$p_1$$$, $$$p_2$$$, $$$p_3$$$ and $$$p_4$$$ on $$$\mathit{XY}$$$ grid.
In one step you can choose one of the points $$$p_i$$$ and move it in one of four directions by one. In other words, if you have chosen point $$$p_i = (x, y)$$$ you can move it to $$$(x, y + 1)$$$, $$$(x, y - 1)$$$, $$$(x + 1, y)$$$ or $$$(x - 1, y)$$$.
Your goal to move points in such a way that they will form a square with sides parallel to $$$\mathit{OX}$$$ and $$$\mathit{OY}$$$ axes (a square with side $$$0$$$ is allowed).
What is the minimum number of steps you need to make such a square?
The first line contains a single integer $$$t$$$ ($$$1 \le t \le 10^4$$$) — the number of test cases.
Each test case consists of four lines. Each line contains two integers $$$x$$$ and $$$y$$$ ($$$0 \le x, y \le 10^9$$$) — coordinates of one of the points $$$p_i = (x, y)$$$.
All points are different in one test case.
For each test case, print the single integer — the minimum number of steps to make a square.
3 0 2 4 2 2 0 2 4 1 0 2 0 4 0 6 0 1 6 2 2 2 5 4 1
8 7 5
In the first test case, one of the optimal solutions is shown below:
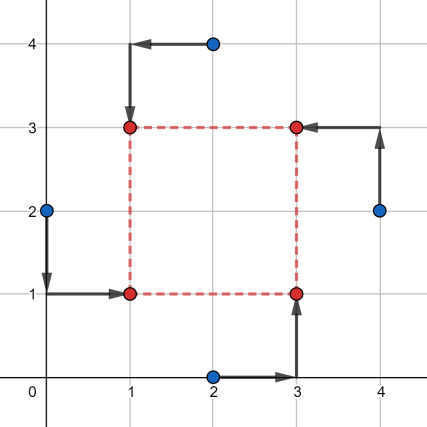
In the second test case, one of the optimal solutions is shown below:
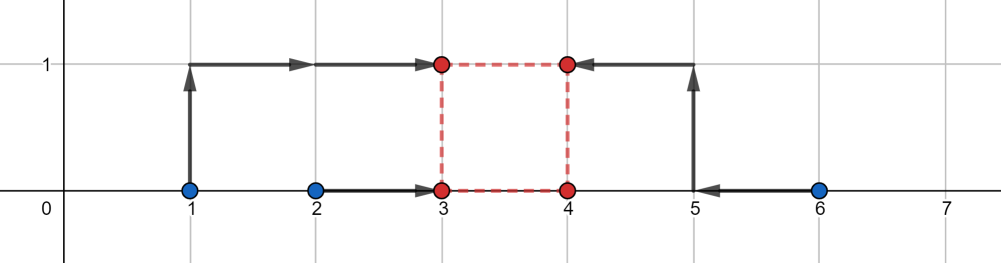
In the third test case, one of the optimal solutions is shown below:

| Name |
|---|




