| Codeforces Global Round 13 |
|---|
| Finished |
Yuezheng Ling gives Luo Tianyi a tree which has $$$n$$$ nodes, rooted at $$$1$$$.
Luo Tianyi will tell you that the parent of the $$$i$$$-th node is $$$a_i$$$ ($$$1 \leq a_i<i$$$ for $$$2 \le i \le n$$$), and she will ask you to perform $$$q$$$ queries of $$$2$$$ types:
- She'll give you three integers $$$l$$$, $$$r$$$ and $$$x$$$ ($$$2 \le l \le r \le n$$$, $$$1 \le x \le 10^5$$$). You need to replace $$$a_i$$$ with $$$\max(a_i-x,1)$$$ for all $$$i$$$ with $$$l \leq i \leq r$$$.
- She'll give you two integers $$$u$$$, $$$v$$$ ($$$1 \le u, v \le n$$$). You need to find the LCA of nodes $$$u$$$ and $$$v$$$ (their lowest common ancestor).
The first line contains two integers $$$n$$$ and $$$q$$$ ($$$2\leq n,q \leq 10^5$$$) — the number of nodes and the number of queries, respectively.
The second line contains $$$n-1$$$ integers $$$a_2, a_3,\dots, a_n$$$ ($$$1 \le a_i < i$$$), where $$$a_i$$$ is the parent of the node $$$i$$$.
Next $$$q$$$ lines contain queries. For each query, the first integer of each line is $$$t$$$ ($$$t = 1$$$ or $$$2$$$) — the type of the query.
If $$$t = 1$$$, this represents the query of the first type. Then, three integers will follow: $$$l$$$, $$$r$$$, $$$x$$$ ($$$2 \le l \le r \le n$$$, $$$1 \le x \le 10^5$$$), meaning that you have to replace $$$a_i$$$ with $$$\max(a_i-x,1)$$$ for all $$$i$$$ with $$$l \leq i \leq r$$$.
If $$$t = 2$$$, this represents the query of the second type. Then, two integers will follow: $$$u$$$ and $$$v$$$ ($$$1 \le u, v \le n$$$), and you have to find the LCA of $$$u$$$ and $$$v$$$.
It's guaranteed that there is at least one query of the second type.
For each query of the second type output answer on a new line.
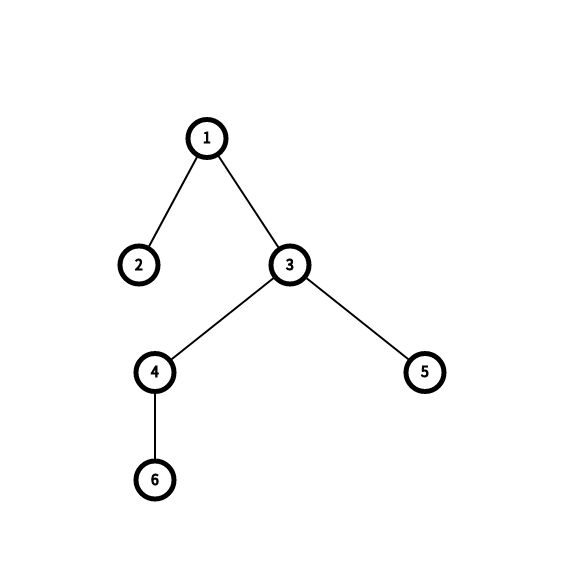
6 4 1 2 3 3 4 2 3 4 1 2 3 1 2 5 6 2 2 3
3 3 1
The tree in example is shown below.

After the query of the first type, the tree changes and is looking as shown below.
| Name |
|---|




