| Codeforces Round 706 (Div. 1) |
|---|
| Закончено |
Будем говорить, что остовное дерево некоторого графа является деревом поиска в ширину с корнем в вершине $$$s$$$, если и только если для всех вершин $$$t$$$ кратчайшее расстояние между вершинами $$$s$$$ и $$$t$$$ в графе равно кратчайшему расстоянию между $$$s$$$ и $$$t$$$ в этом остовном дереве.
Для фиксированного графа можно определить $$$f(x,y)$$$ как число остовных деревьев в данном графе таких, что они являются деревьями поиска в ширину как с корнем в $$$x$$$, так и с корнем в $$$y$$$.
Вам дан неориентированный связный граф с $$$n$$$ вершинами и $$$m$$$ ребрами. Вычислите $$$f(i,j)$$$ для всех $$$i$$$, $$$j$$$ по модулю $$$998\,244\,353$$$.
Первая строка содержит два целых числа $$$n$$$ и $$$m$$$ ($$$1 \le n \le 400$$$, $$$0 \le m \le 600$$$) — количество вершин и ребер в графе.
$$$i$$$-я из следующих $$$m$$$ строк содержит два целых числа $$$a_i$$$, $$$b_i$$$ ($$$1 \leq a_i, b_i \leq n$$$, $$$a_i < b_i$$$), описывающих ребро, соединяющее $$$a_i$$$ и $$$b_i$$$.
Гарантируется, что все ребра различны, а граф — связный.
Выведите $$$n$$$ строк, каждая из которых содержит $$$n$$$ целых чисел.
Число в строке $$$i$$$ на позиции $$$j$$$ должно быть равно $$$f(i,j) \bmod 998\,244\,353$$$.
4 4 1 2 2 3 3 4 1 4
2 1 0 1 1 2 1 0 0 1 2 1 1 0 1 2
8 9 1 2 1 3 1 4 2 7 3 5 3 6 4 8 2 3 3 4
1 0 0 0 0 0 0 0 0 2 0 0 0 0 2 0 0 0 1 0 1 1 0 0 0 0 0 2 0 0 0 2 0 0 1 0 1 1 0 0 0 0 1 0 1 1 0 0 0 2 0 0 0 0 2 0 0 0 0 2 0 0 0 2
Изображения ниже описывают первый пример.
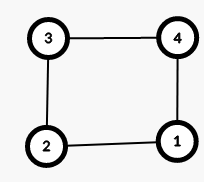
Дерево из красных ребер является деревом поиска в ширину с корнем как в $$$1$$$, так и в $$$2$$$.
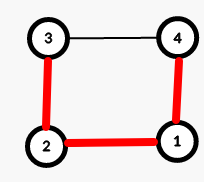
Похожим образом можно построить деревья поисков в ширину для любой пары соседних вершин.
| Название |
|---|




