| 2020-2021 ICPC, NERC, Northern Eurasia Onsite (Unrated, Online Mirror, ICPC Rules, Teams Preferred) |
|---|
| Finished |
Imagine a board with $$$n$$$ pins put into it, the $$$i$$$-th pin is located at $$$(x_i, y_i)$$$. For simplicity, we will restrict the problem to the case where the pins are placed in vertices of a convex polygon.
Then, take a non-stretchable string of length $$$l$$$, and put it around all the pins. Place a pencil inside the string and draw a curve around the pins, trying to pull the string in every possible direction. The picture below shows an example of a string tied around the pins and pulled by a pencil (a point $$$P$$$).
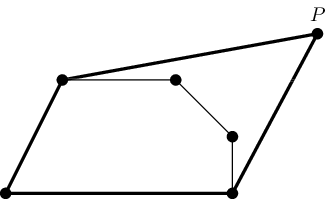
Your task is to find an area inside this curve. Formally, for a given convex polygon $$$S$$$ and a length $$$l$$$ let's define a fiber shape $$$F(S, l)$$$ as a set of points $$$t$$$ such that the perimeter of the convex hull of $$$S \cup \{t\}$$$ does not exceed $$$l$$$. Find an area of $$$F(S, l)$$$.
The first line contains two integers $$$n$$$ and $$$l$$$ ($$$3 \le n \le 10^4$$$; $$$1 \le l \le 8 \cdot 10^5$$$) — the number of vertices of the polygon $$$S$$$ and the length of the string. Next $$$n$$$ lines contain integers $$$x_i$$$ and $$$y_i$$$ ($$$-10^5 \le x_i, y_i \le 10^5$$$) — coordinates of polygon's vertices in counterclockwise order. All internal angles of the polygon are strictly less than $$$\pi$$$. The length $$$l$$$ exceeds the perimeter of the polygon by at least $$$10^{-3}$$$.
Output a single floating-point number — the area of the fiber shape $$$F(S, l)$$$. Your answer will be considered correct if its absolute or relative error doesn't exceed $$$10^{-6}$$$.
3 4 0 0 1 0 0 1
3.012712585980357
4 5 0 0 1 0 1 1 0 1
5.682061989789656
5 17 0 0 2 -1 3 0 4 3 -1 4
37.719371276930820
The following pictures illustrate the example tests.



| Name |
|---|




