| Codeforces Round 810 (Div. 1) |
|---|
| Finished |
A picture can be represented as an $$$n\times m$$$ grid ($$$n$$$ rows and $$$m$$$ columns) so that each of the $$$n \cdot m$$$ cells is colored with one color. You have $$$k$$$ pigments of different colors. You have a limited amount of each pigment, more precisely you can color at most $$$a_i$$$ cells with the $$$i$$$-th pigment.
A picture is considered beautiful if each cell has at least $$$3$$$ toroidal neighbors with the same color as itself.
Two cells are considered toroidal neighbors if they toroidally share an edge. In other words, for some integers $$$1 \leq x_1,x_2 \leq n$$$ and $$$1 \leq y_1,y_2 \leq m$$$, the cell in the $$$x_1$$$-th row and $$$y_1$$$-th column is a toroidal neighbor of the cell in the $$$x_2$$$-th row and $$$y_2$$$-th column if one of following two conditions holds:
- $$$x_1-x_2 \equiv \pm1 \pmod{n}$$$ and $$$y_1=y_2$$$, or
- $$$y_1-y_2 \equiv \pm1 \pmod{m}$$$ and $$$x_1=x_2$$$.
Notice that each cell has exactly $$$4$$$ toroidal neighbors. For example, if $$$n=3$$$ and $$$m=4$$$, the toroidal neighbors of the cell $$$(1, 2)$$$ (the cell on the first row and second column) are: $$$(3, 2)$$$, $$$(2, 2)$$$, $$$(1, 3)$$$, $$$(1, 1)$$$. They are shown in gray on the image below:
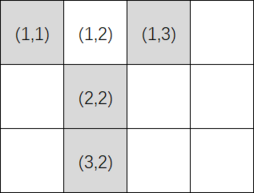 The gray cells show toroidal neighbors of $$$(1, 2)$$$.
The gray cells show toroidal neighbors of $$$(1, 2)$$$. Is it possible to color all cells with the pigments provided and create a beautiful picture?
Each test contains multiple test cases. The first line contains the number of test cases $$$t$$$ ($$$1 \leq t \leq 10^4$$$). The description of the test cases follows.
The first line of each test case contains three integers $$$n$$$, $$$m$$$, and $$$k$$$ ($$$3 \leq n,m \leq 10^9$$$, $$$1 \leq k \leq 10^5$$$) — the number of rows and columns of the picture and the number of pigments.
The next line contains $$$k$$$ integers $$$a_1,a_2,\dots, a_k$$$ ($$$1 \leq a_i \leq 10^9$$$) — $$$a_i$$$ is the maximum number of cells that can be colored with the $$$i$$$-th pigment.
It is guaranteed that the sum of $$$k$$$ over all test cases does not exceed $$$10^5$$$.
For each test case, print "Yes" (without quotes) if it is possible to color a beautiful picture. Otherwise, print "No" (without quotes).
64 6 312 9 83 3 28 83 3 29 54 5 210 115 4 29 1110 10 311 45 14
Yes No Yes Yes No No
In the first test case, one possible solution is as follows:

In the third test case, we can color all cells with pigment $$$1$$$.
| Name |
|---|




