You are given an undirected, connected graph of $$$n$$$ nodes and $$$m$$$ edges. All nodes $$$u$$$ of the graph satisfy the following:
- Let $$$S_u$$$ be the set of vertices in the longest simple cycle starting and ending at $$$u$$$.
- Let $$$C_u$$$ be the union of the sets of vertices in any simple cycle starting and ending at $$$u$$$.
- $$$S_u = C_u$$$.
You need to answer $$$q$$$ queries.
For each query, you will be given node $$$a$$$ and node $$$b$$$. Out of all the edges that belong to any simple path from $$$a$$$ to $$$b$$$, count the number of edges such that if you remove that edge, $$$a$$$ and $$$b$$$ are reachable from each other.
The first line contains two integers $$$n$$$ and $$$m$$$ ($$$2 \le n \le 2 \cdot 10^5$$$, $$$1 \le m \le \min$$$($$$2 \cdot 10^5$$$, $$$(n \cdot (n-1))/2$$$)) — the total number of nodes and edges in the graph, respectively.
The next $$$m$$$ lines contain two integers $$$u$$$ and $$$v$$$ ($$$1 \le$$$ $$$u$$$, $$$v$$$ $$$\le n$$$, $$$u \neq v$$$) — describing an edge, implying that nodes $$$u$$$ and $$$v$$$ are connected to each other.
It is guaranteed that there is at most one edge between any pair of vertices in the graph and the given graph is connected.
The next line contains a single integer $$$q$$$ ($$$1 \le q \le 2 \cdot 10^5$$$) — the number of queries.
Then $$$q$$$ lines follow, each representing a query. Each query contains two integers $$$a$$$ and $$$b$$$ ($$$1 \le$$$ $$$a$$$, $$$b$$$ $$$\le n$$$).
For each query, output a single integer — answer to the query.
10 11 1 2 2 3 3 4 4 5 5 3 2 7 7 9 9 10 10 6 6 7 1 8 5 1 4 5 10 3 5 2 8 7 10
3 7 3 0 4
13 15 1 2 2 3 3 4 4 1 2 4 3 5 5 6 6 7 6 8 7 9 9 10 8 7 10 11 10 12 10 13 6 9 11 1 5 1 8 5 2 5 12 12 13
0 5 8 5 3 0
The graph in the first sample is :
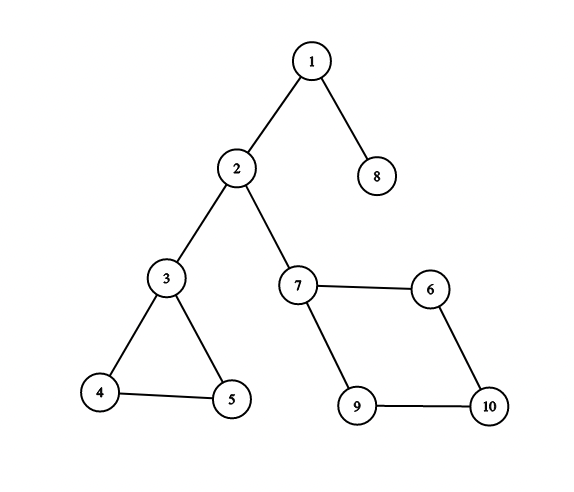
The first query is $$$(1, 4)$$$. There are $$$5$$$ total edges that belong to any simple path from $$$1$$$ to $$$4$$$. Edges $$$(3, 4), (4, 5), (5, 3)$$$ will be counted in the answer to the query.
The fourth query is $$$(2, 8)$$$. There is only one simple path from $$$2$$$ to $$$8$$$, thus none of the edges will be counted in the answer to the query.
The fifth query is $$$(7, 10)$$$. There are $$$4$$$ total edges that belong to any simple path from $$$7$$$ to $$$10$$$, all of them will be counted in the answer to the query.
| Name |
|---|




