You are given a tree of $$$n$$$ nodes, rooted at $$$1$$$. Every node has a value of either $$$0$$$ or $$$1$$$ at time $$$t=0$$$.
At any integer time $$$t>0$$$, the value of a node becomes the bitwise XOR of the values of its children at time $$$t - 1$$$; the values of leaves become $$$0$$$ since they don't have any children.
Let $$$S(t)$$$ denote the sum of values of all nodes at time $$$t$$$.
Let $$$F(A)$$$ denote the sum of $$$S(t)$$$ across all values of $$$t$$$ such that $$$0 \le t \le 10^{100}$$$, where $$$A$$$ is the initial assignment of $$$0$$$s and $$$1$$$s in the tree.
The task is to find the sum of $$$F(A)$$$ for all $$$2^n$$$ initial configurations of $$$0$$$s and $$$1$$$s in the tree. Print the sum modulo $$$10^9+7$$$.
Each test contains multiple test cases. The first line contains the number of test cases $$$t$$$ ($$$1 \le t \le 10^5$$$). The description of the test cases follows.
The first line of each test case contains $$$n$$$ ($$$1 \le n \le 2 \cdot 10^5$$$) — the number of nodes in the tree.
The next $$$n-1$$$ lines of each test case contain two integers each — $$$u$$$, $$$v$$$ indicating an edge between $$$u$$$ and $$$v$$$ ($$$1 \le u, v \le n$$$).
It is guaranteed that the sum of $$$n$$$ over all test cases does not exceed $$$2 \cdot 10^5$$$.
Output the sum modulo $$$10^9+7$$$ for each test case.
161 21 33 43 53 6
288
Let us find $$$F(A)$$$ for the configuration $$$A = [0,1,0,0,1,1]$$$ ($$$A[i]$$$ denotes the value of node $$$i$$$). Initially (at $$$t = 0$$$) our tree is as shown in the picture below. In each node, two values are shown: the number and the value of this node. $$$S(0)$$$ for this configuration is $$$3$$$.
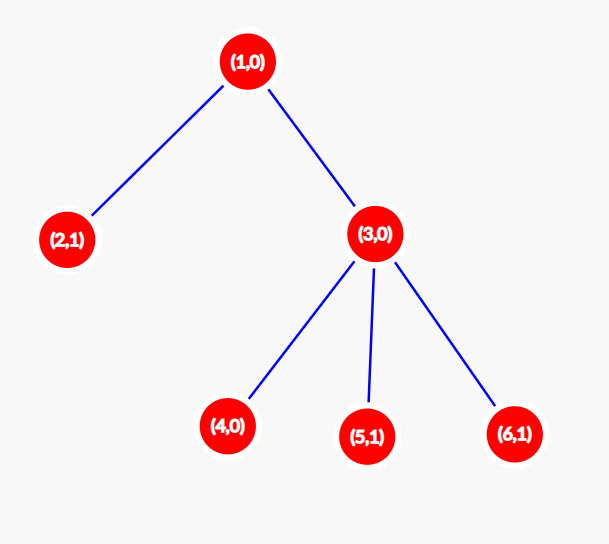
At $$$t = 1$$$ the configuration changes to $$$[1,0,0,0,0,0]$$$. The tree looks as shown below. $$$S(1) = 1$$$.
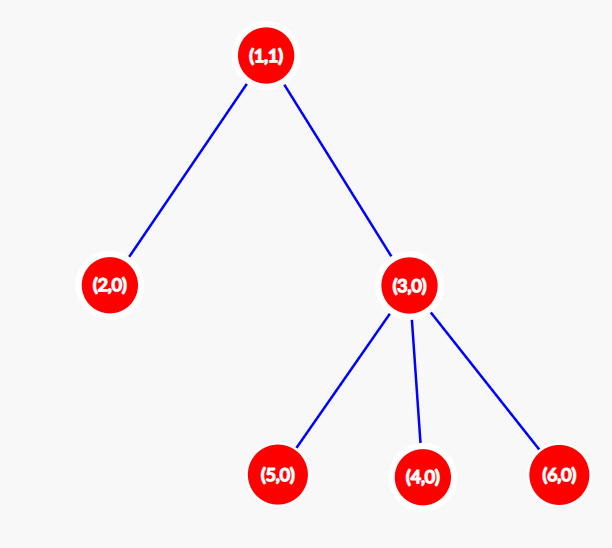
At $$$t = 2$$$ the configuration changes to $$$[0,0,0,0,0,0]$$$. The tree looks as shown below. $$$S(2) = 0$$$.
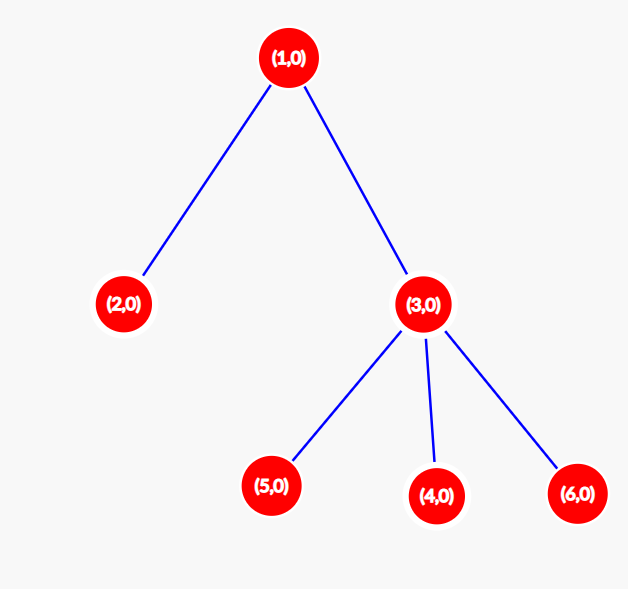
For all $$$t>2$$$, the graph remains unchanged, so $$$S(t)=0$$$ for all $$$t > 2$$$. So, for the initial configuration $$$A = [0,1,0,0,1,1]$$$, the value of $$$F(A) = 3 + 1 = 4$$$.
Doing this process for all possible $$$2^{6}$$$ configurations yields us an answer of $$$\textbf{288}$$$.
| Name |
|---|




