| Codeforces Round 872 (Div. 1) |
|---|
| Finished |
LuoTianyi gives you a tree with values in its vertices, and the root of the tree is vertex $$$1$$$.
In one operation, you can change the value in one vertex to any non-negative integer.
Now you need to find the minimum number of operations you need to perform to make each path from the root to leaf$$$^{\dagger}$$$ has a bitwise XOR value of zero.
$$$^{\dagger}$$$A leaf in a rooted tree is a vertex that has exactly one neighbor and is not a root.
The first line contains a single integer $$$n$$$ ($$$2 \le n \le 10^5$$$) — the number of vertices in the tree.
The second line contains $$$n$$$ integers $$$a_1, a_2, \ldots, a_n$$$ ($$$1 \le a_i \le 10^9$$$), the $$$i$$$-th number represents the value in the $$$i$$$-th vertex.
Next $$$n−1$$$ lines describe the edges of the tree. The $$$i$$$-th line contains two integers $$$u_i$$$ and $$$v_i$$$ ($$$1 \le u_i,v_i \le n, u_i \neq v_i$$$) — the vertices connected by an edge of the tree. It's guaranteed that the given edges form a tree.
Print a single integer — the minimum number of operations.
6 3 5 7 5 8 4 1 2 1 3 1 4 3 5 4 6
3
8 7 10 7 16 19 9 16 11 1 5 4 2 6 5 5 2 7 2 2 3 3 8
3
4 1 2 1 2 1 2 2 3 4 3
0
9 4 3 6 1 5 5 5 2 7 1 2 2 3 4 1 4 5 4 6 4 7 8 1 8 9
2
The tree in the first example:
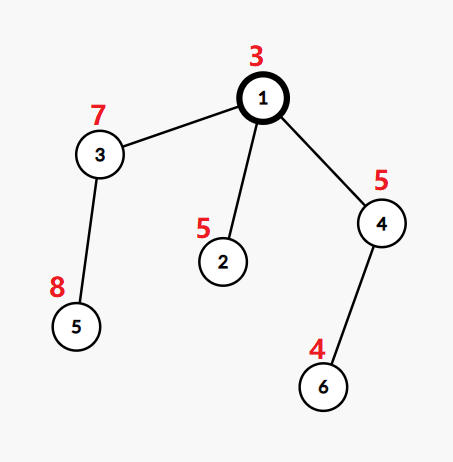
If we change the value in the vertex $$$2$$$ to $$$3$$$, the value in the vertex $$$5$$$ to $$$4$$$, and the value in the vertex $$$6$$$ to $$$6$$$, then the tree will be ok.
The bitwise XOR from the root to the leaf $$$2$$$ will be $$$3 \oplus 3=0$$$.
The bitwise XOR from the root to the leaf $$$5$$$ will be $$$4 \oplus 7 \oplus 3=0$$$.
The bitwise XOR from the root to the leaf $$$6$$$ will be $$$6 \oplus 5 \oplus 3=0$$$.
The tree in the second example:

If we change the value in the vertex $$$2$$$ to $$$4$$$, the value in the vertex $$$3$$$ to $$$27$$$, and the value in the vertex $$$6$$$ to $$$20$$$, then the tree will be ok.
The bitwise XOR from the root to the leaf $$$6$$$ will be $$$20 \oplus 19 \oplus 7=0$$$.
The bitwise XOR from the root to the leaf $$$8$$$ will be $$$11 \oplus 27 \oplus 4 \oplus 19 \oplus 7=0$$$.
The bitwise XOR from the root to the leaf $$$4$$$ will be $$$16 \oplus 4 \oplus 19 \oplus 7=0$$$.
The bitwise XOR from the root to the leaf $$$7$$$ will be $$$16 \oplus 4 \oplus 19 \oplus 7=0$$$.
In the third example, the only leaf is the vertex $$$4$$$ and the bitwise XOR on the path to it is $$$1 \oplus 2 \oplus 1 \oplus 2 = 0$$$, so we don't need to change values.
In the fourth example, we can change the value in the vertex $$$1$$$ to $$$5$$$, and the value in the vertex $$$4$$$ to $$$0$$$.
Here $$$\oplus$$$ denotes the bitwise XOR operation.
| Name |
|---|




