| Codeforces Round 449 (Div. 1) |
|---|
| Finished |
— Willem...
— What's the matter?
— It seems that there's something wrong with Seniorious...
— I'll have a look...

Seniorious is made by linking special talismans in particular order.
After over 500 years, the carillon is now in bad condition, so Willem decides to examine it thoroughly.
Seniorious has n pieces of talisman. Willem puts them in a line, the i-th of which is an integer ai.
In order to maintain it, Willem needs to perform m operations.
There are four types of operations:
- 1 l r x: For each i such that l ≤ i ≤ r, assign ai + x to ai.
- 2 l r x: For each i such that l ≤ i ≤ r, assign x to ai.
- 3 l r x: Print the x-th smallest number in the index range [l, r], i.e. the element at the x-th position if all the elements ai such that l ≤ i ≤ r are taken and sorted into an array of non-decreasing integers. It's guaranteed that 1 ≤ x ≤ r - l + 1.
- 4 l r x y: Print the sum of the x-th power of ai such that l ≤ i ≤ r, modulo y, i.e.
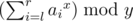 .
.
The only line contains four integers n, m, seed, vmax (1 ≤ n, m ≤ 105, 0 ≤ seed < 109 + 7, 1 ≤ vmax ≤ 109).
The initial values and operations are generated using following pseudo code:
def rnd():
ret = seed
seed = (seed * 7 + 13) mod 1000000007
return ret
for i = 1 to n:
a[i] = (rnd() mod vmax) + 1
for i = 1 to m:
op = (rnd() mod 4) + 1
l = (rnd() mod n) + 1
r = (rnd() mod n) + 1
if (l > r):
swap(l, r)
if (op == 3):
x = (rnd() mod (r - l + 1)) + 1
else:
x = (rnd() mod vmax) + 1
if (op == 4):
y = (rnd() mod vmax) + 1
Here op is the type of the operation mentioned in the legend.
For each operation of types 3 or 4, output a line containing the answer.
10 10 7 9
2
1
0
3
10 10 9 9
1
1
3
3
In the first example, the initial array is {8, 9, 7, 2, 3, 1, 5, 6, 4, 8}.
The operations are:
- 2 6 7 9
- 1 3 10 8
- 4 4 6 2 4
- 1 4 5 8
- 2 1 7 1
- 4 7 9 4 4
- 1 2 7 9
- 4 5 8 1 1
- 2 5 7 5
- 4 3 10 8 5
| Name |
|---|




