Priests of the Quetzalcoatl cult want to build a tower to represent a power of their god. Tower is usually made of power-charged rocks. It is built with the help of rare magic by levitating the current top of tower and adding rocks at its bottom. If top, which is built from k - 1 rocks, possesses power p and we want to add the rock charged with power wk then value of power of a new tower will be {wk}p.
Rocks are added from the last to the first. That is for sequence w1, ..., wm value of power will be
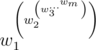
After tower is built, its power may be extremely large. But still priests want to get some information about it, namely they want to know a number called cumulative power which is the true value of power taken modulo m. Priests have n rocks numbered from 1 to n. They ask you to calculate which value of cumulative power will the tower possess if they will build it from rocks numbered l, l + 1, ..., r.
First line of input contains two integers n (1 ≤ n ≤ 105) and m (1 ≤ m ≤ 109).
Second line of input contains n integers wk (1 ≤ wk ≤ 109) which is the power of rocks that priests have.
Third line of input contains single integer q (1 ≤ q ≤ 105) which is amount of queries from priests to you.
kth of next q lines contains two integers lk and rk (1 ≤ lk ≤ rk ≤ n).
Output q integers. k-th of them must be the amount of cumulative power the tower will have if is built from rocks lk, lk + 1, ..., rk.
6 1000000000
1 2 2 3 3 3
8
1 1
1 6
2 2
2 3
2 4
4 4
4 5
4 6
1
1
2
4
256
3
27
597484987
327 = 7625597484987
| Name |
|---|




