In the NN country, there are $$$n$$$ cities, numbered from $$$1$$$ to $$$n$$$, and $$$n - 1$$$ roads, connecting them. There is a roads path between any two cities.
There are $$$m$$$ bidirectional bus routes between cities. Buses drive between two cities taking the shortest path with stops in every city they drive through. Travelling by bus, you can travel from any stop on the route to any other. You can travel between cities only by bus.
You are interested in $$$q$$$ questions: is it possible to get from one city to another and what is the minimum number of buses you need to use for it?
The first line contains a single integer $$$n$$$ ($$$2 \le n \le 2 \cdot 10^5$$$) — the number of cities.
The second line contains $$$n - 1$$$ integers $$$p_2, p_3, \ldots, p_n$$$ ($$$1 \le p_i < i$$$), where $$$p_i$$$ means that cities $$$p_i$$$ and $$$i$$$ are connected by road.
The third line contains a single integer $$$m$$$ ($$$1 \le m \le 2 \cdot 10^5$$$) — the number of bus routes.
Each of the next $$$m$$$ lines contains $$$2$$$ integers $$$a$$$ and $$$b$$$ ($$$1 \le a, b \le n$$$, $$$a \neq b$$$), meaning that there is a bus route between cities $$$a$$$ and $$$b$$$. It is possible that there is more than one route between two cities.
The next line contains a single integer $$$q$$$ ($$$1 \le q \le 2 \cdot 10^5$$$) — the number of questions you are interested in.
Each of the next $$$q$$$ lines contains $$$2$$$ integers $$$v$$$ and $$$u$$$ ($$$1 \le v, u \le n$$$, $$$v \neq u$$$), meaning that you are interested if it is possible to get from city $$$v$$$ to city $$$u$$$ and what is the minimum number of buses you need to use for it.
Print the answer for each question on a separate line. If there is no way to get from one city to another, print $$$-1$$$. Otherwise print the minimum number of buses you have to use.
7
1 1 1 4 5 6
4
4 2
5 4
1 3
6 7
6
4 5
3 5
7 2
4 5
3 2
5 3
1
3
-1
1
2
3
7
1 1 2 3 4 1
4
4 7
3 5
7 6
7 6
6
4 6
3 1
3 2
2 7
6 3
5 3
1
-1
-1
1
-1
1
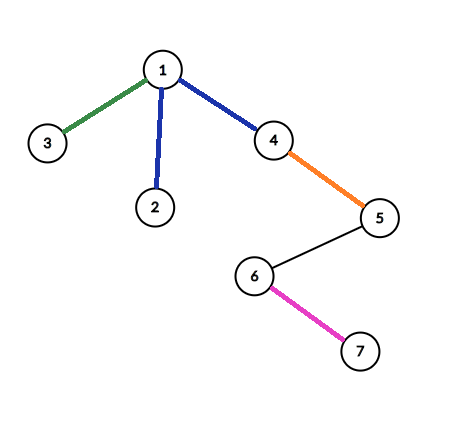 Routes for first sample are marked on the picture.
Routes for first sample are marked on the picture.
| Name |
|---|




