| acmsguru |
|---|
| Finished |
→ Problem tags
No tags yet
No tag edit access
The problem statement has recently been changed. View the changes.
×
489. Extremal Permutations
Time limit per test: 0.5 second(s)
Memory limit: 262144 kilobytes
Memory limit: 262144 kilobytes
input: standard
output: standard
output: standard
A member ai of the sequence a1, a2, ·s, an is called a
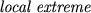 if either ai > ai-1 and ai > ai+1 (local maximum) or ai < ai-1 and ai < ai+1 (local minimum). A sequence p1, p2, ·s, pn is called a
if either ai > ai-1 and ai > ai+1 (local maximum) or ai < ai-1 and ai < ai+1 (local minimum). A sequence p1, p2, ·s, pn is called a 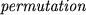 of the integers from 1 to n if each of the integers appears in the sequence exactly once. A permutation is called
of the integers from 1 to n if each of the integers appears in the sequence exactly once. A permutation is called 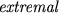 if each member (except the first and the last) is a local extreme.
if each member (except the first and the last) is a local extreme.Compute the total number of extremal permutations of the integers from 1 to n and output the result modulo m.
Input
The first and only line of the input file contains the integers n (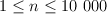 ) and m (1 ≤ m ≤ 109).
) and m (1 ≤ m ≤ 109).Output
The output file should contain a single integer, the remainder from division of the total number of extremal permutations of integers from 1 to n by the given integer m.Example(s)
sample input | sample output |
3 10 | 4 |
sample input | sample output |
3 3 | 1 |
Note. The extremal permutations of 1·s3 are (1, 3, 2), (2, 1, 3), (2, 3, 1) and (3, 1, 2).
Codeforces (c) Copyright 2010-2024 Mike Mirzayanov
The only programming contests Web 2.0 platform
Server time: Apr/23/2024 22:05:45 (f1).
Desktop version, switch to mobile version.
Supported by
User lists


| Name |
|---|




