| acmsguru |
|---|
| Finished |
→ Problem tags
No tags yet
No tag edit access
The problem statement has recently been changed. View the changes.
×
513. Maximal Clique
Time limit per test: 0.25 second(s)
Memory limit: 262144 kilobytes
Memory limit: 262144 kilobytes
input: standard
output: standard
output: standard
This is the moment you've been waiting for all your life: you've invented a way to quickly solve the Maximal Clique problem: given an undirected graph find the size of the maximal subset of its vertices that form a clique (are pairwise connected). This problem is NP-hard, meaning you've got a proof that P=NP!
Unfortunately, the scientific community is not so eager to listen to you. Your papers on the subject are being rejected because of "solving an obviously unsolvable problem". Your phone number is already on the ignore list of all Computer Science professors you know. The world seems to hate you.
So you've decided to create a solver for the Maximal Clique problem and put it online, so that everyone can check for himself that you're right. You've already implemented the solver and almost launched the website, but then you've realized that this is not a very good idea: if you make the solver available, everyone will be able to solve every problem from NP by reducing it to the Maximal Clique problem. What if people will just silently use it instead of bringing you fame and respect?
Luckily, the only proof of NP-hardness of the Maximal Clique problem you know works by reducing the 3-SAT problem to it in a very specific way. So you've decided to check if the input graph given to your solver could be obtained from this reduction, and if yes, refuse to solve the problem. That way, nobody will be able to get quick solutions for all problems from NP, but everyone will still be able to verify your solver by feeding other graphs to it.
3-SAT problem statement is: given a formula of form
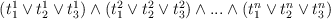 , where each term tji is either some boolean variable or its negation (more formally, either xk or
, where each term tji is either some boolean variable or its negation (more formally, either xk or 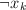 ), check whether there exists some assignment of true/false values to each variable so that the formula evaluates to true. All three terms in one clause must represent different variables.
), check whether there exists some assignment of true/false values to each variable so that the formula evaluates to true. All three terms in one clause must represent different variables.The reduction works in the following manner. From the above formula, we create a graph with 3n vertices, one for each variable of each clause. Two vertices corresponding to terms tji and tsr are connected when i ≠ r (so the terms belong to different clauses) and those terms are non-contradictory (they are either equal or represent different variables).
The following picture shows the resulting graph for the formula
 :
:
Given a graph, you need to check if it could be created by the above reduction. The vertices are permuted arbitrarily.
Input
The first line of the input file contains two integers v and e, 1 ≤ v ≤ 100, denoting the number of vertices and edges in the graph. The next e lines contain two integers each, denoting the numbers of vertices connected by an edge. Each pair of vertices are connected at most once, no edge connects a vertex to itself.Output
Output "YES" when the given graph could be obtained by the given reduction, or "NO" otherwise.Example(s)
sample input | sample output |
9 22 1 3 1 6 7 1 8 9 9 1 2 3 2 4 2 5 2 6 2 8 3 4 3 5 3 7 4 8 4 9 5 6 5 7 5 8 5 9 6 7 6 9 7 8 | YES |
Codeforces (c) Copyright 2010-2024 Mike Mirzayanov
The only programming contests Web 2.0 platform
Server time: Apr/20/2024 06:31:04 (k1).
Desktop version, switch to mobile version.
Supported by
User lists


| Name |
|---|




