Thanks everybody for participating. Tasks follow in the order of the original contest (the mirror order is given in the brackets).
The editorial is being translated right now. The Russian text is in italic.
562A - Logistical Questions
(in mirror: 566C - Logistical Questions)
Let's think about formal statement of the problem. We are given a tricky definition of a distance on the tre: ρ(a, b) = dist(a, b)1.5. Each vertex has its weight wi. We need to choose a place x for a competition such that the sum of distances from all vertices of the tree with their weights is minimum possible: f(x) = w1ρ(1, x) + w2ρ(x, 2) + ... + wnρ(x, n).
Let's understand how function f(x) works. Allow yourself to put point x not only in vertices of the tree, but also in any point inside each edge by naturally expanding the distance definition (for example, the middle of the edge of length 4 km is located 2 km from both ends of this edge).
Fact 1. For any path 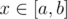 in the tree the function ρ(i, x) is convex. Actually, the function dist(i, x) plot on each path [a, b] looks like the plot of a function abs(x): it first decreases linearly to the minimum: the closes to i point on a segment [a, b], and then increases linearly. Taking a composition with a convex increasing function t1.5, as we can see, we get the convex function on any path in the tree. Here by function on the path we understand usual function of a real variable x that is identified with its location on path x: dist(a, x). So, each of the summands in the definition of f(x) is convex on any path in the tree, so f(x) is also convex on any path in the tree.
in the tree the function ρ(i, x) is convex. Actually, the function dist(i, x) plot on each path [a, b] looks like the plot of a function abs(x): it first decreases linearly to the minimum: the closes to i point on a segment [a, b], and then increases linearly. Taking a composition with a convex increasing function t1.5, as we can see, we get the convex function on any path in the tree. Here by function on the path we understand usual function of a real variable x that is identified with its location on path x: dist(a, x). So, each of the summands in the definition of f(x) is convex on any path in the tree, so f(x) is also convex on any path in the tree.
Let's call convex functions on any path in the tree convex on tree. Let's formulate few facts about convex functions on trees.
Fact 2. A convex function on tree can't have two different local minimums. Indeed, otherwise the path between those minimums contradicts the property of being convex on any path in the tree.
So, any convex function f(x) on the tree has the only local minimum that coincides with its global minimum.
Fact 3. From each vertex v there exists no more than one edge in which direction the function f decreases. Indeed, otherwise the path connecting two edges of function decrease would contradict the definition of a convex function in a point v.
Let's call such edge that function decreases along this edge to be a gradient of function f in point x. By using facts 2 and 3 we see that in each vertex there is either a uniquely defined gradient or the vertex is a global minimum.
Suppose we are able to efficiently find a gradient direction by using some algorithm for a given vertex v. If our tree was a bamboo then the task would be a usual convex function minimization that is efficiently solved by a binary search, i. e. dichotomy. We need some equivalent of a dichotomy for a tree. What is it?
Let's use centroid decmoposition! Indeed, let's take a tree center (i. e. such vertex that sizes of all its subtrees are no larger than n / 2). By using fact 3 we may consider the gradient of f in the center of the tree. First of all, there may be no gradient in this point meaning that we already found an optimum. Otherwise we know that global minimum is located in a subtree in direction of gradient, so all remaining subtrees and the center can be excluded from our consideration. So, by running one gradient calculation we reduced the number of vertices in a considered part of a tree twice.
So, in  runs of gradient calculation we almost solved the problem. Let's understand where exactly the answer is located. Note that the global optimum will most probably be located inside some edge. It is easy to see that the optimum vertex will be one of the vertices incident to that edge, or more specifically, one of the last two considered vertices by our algorithms. Which exactly can be determined by calculating the exact answer for them and choosing the most optimal among them.
runs of gradient calculation we almost solved the problem. Let's understand where exactly the answer is located. Note that the global optimum will most probably be located inside some edge. It is easy to see that the optimum vertex will be one of the vertices incident to that edge, or more specifically, one of the last two considered vertices by our algorithms. Which exactly can be determined by calculating the exact answer for them and choosing the most optimal among them.
Now let's calculate the gradient direction in a vertex v. Fix a subtree ui of a vertex v. Consider a derivative of all summands from that subtree when we move into that subtree. Denote this derivative as deri. Then, as we can see, the derivative of f(x) while moving from x = v in direction of subtree ui is - der1 - der2 - ... - deri - 1 + deri - deri + 1 - ... - derk where k is a degree of vertex v. So, by running one DFS from vertex v we may calculate all values deri, and so we may find a gradient direction by applying the formula above and considering a direction with negative derivative.
Finally, we got a solution in  .
.
562B - Clique in the Divisibility Graph
(in mirror: 566F - Clique in the Divisibility Graph)
Order numbers in the sought clique in ascending order. Note that set X = {x1, ..., xk} is a clique iff 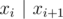 for (1 ≤ i ≤ k - 1). So, it's easy to formulate a dynamic programming problem: D[x] is equal to the length of a longest suitable increasing subsequence ending in a number x. The calculation formula:
for (1 ≤ i ≤ k - 1). So, it's easy to formulate a dynamic programming problem: D[x] is equal to the length of a longest suitable increasing subsequence ending in a number x. The calculation formula: 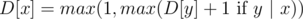 for all x in set A.
for all x in set A.
If DP is written in "forward" direction then it's easy to estimate the complexity of a solution. In the worst case we'll process 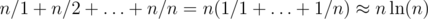 transitions.
transitions.
562C - Restoring Map
(in mirror: 566E - Restoring Map)
Let's call a neighborhood of a vertex — the set consisting of it and all vertices near to it. So, we know the set of all neighborhoods of all vertices in some arbitrary order, and also each neighborhood is shuffled in an arbitrary order.
Let's call the tree vertex to be internal if it is not a tree leaf. Similarly, let's call a tree edge to be internal if it connects two internal vertices. An nice observation is that if two neighborhoods intersect exactly by two elements a and b then a and b have to be connected with an edge, in particular the edge (a, b) is internal. Conversely, any internal edge (a, b) may be represented as an intersection of some two neighborhoods С and D of some two vertices c and d such that there is a path c – a – b – d in the tree. In such manner we may find all internal edges by considering pairwise intersections of all neighborhoods. This can be done in about n3 / 2 operations naively, or in 32 times faster, by using bitsets technique.
Note that knowing all internal edges we may determine all internal vertices except the only case of a star graph (i. e. the graph consisting of a vertex with several other vertices attached to it). The case of a star should be considered separately.
Now we know the set of all leaves, all internal vertices and a tree structure on all internal vertices. The only thing that remained is to determine for each leaf, to what internal vertex is should be attached. This can be done in following manner. Consider a leaf l. Consider all neighborhoods containing it. Consider a minimal neighborhood among them; it can be shown that it is exactly the neighborhood L corresponding to a leaf l itself. Consider all internal vertices in L. There can be no less than two of them.
If there are three of them or more then we can uniquely determine to which of them l should be attached — it should be such vertex from them that has a degree inside L larger than 1. If there are exactly two internal vertices in L (let's say, a and b), then determining the attach point for l is a bit harder.
Statement: l should be attached to that vertex among a, b, that has an internal degree exactly 1. Indeed, if l was attached to a vertex with internal degree larger than 1, we would have considered this case before.
If both of vertices a and b have internal degree — 1 then our graph looks like a dumbbell (an edge (a, b) and all remaining vertices attached either to a or to b). Such case should also be considered separately.
The solution for two special cases remains for a reader as an easy exercise.
==== UNTRANSLATED SECTION, PLEASE WAIT A FEW MINUTES... ====

Kitten to take your attention :)
562D - Restructuring Company
(в трансляции: 566D - Restructuring Company)
Эта задача допускает множество решений с разными асимптотиками. Опишем решение за 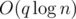 .
.
Рассмотрим сначала задачу, в которой присутствуют только запросы второго и третьего типа. Её можно решить следующим образом. Отметим всех работников в ряд на прямой от 1 до n. Заметим, что отделы представляют собой отрезки из подряд идущих работников. Будем поддерживать эти отрезки в любой логарифмической структуре данных, например в сбалансированном дереве поиска (std::set или TreeSet). Объединяя все отделы с позиции x по позицию y, вытаскиваем все отрезки, попавшие в диапазон [x, y] и сливаем их. Для ответа на запрос третьего типа проверяем, лежат ли работники x и y в одном отрезке. Таким образом, мы получаем решение более простой задачи за  на запрос.
на запрос.
Добавляя запросы первого типа мы на самом деле разрешаем некоторым отрезкам на прямой относиться к одному и тому же отделу. Добавим в решение систему непересекающихся множеств, которая будет поддерживать классы эквивалентности на отрезках. Теперь запросы первого типа можно реализовать как вызов merge в системе непересекающихся множеств от номеров отделов, к которым принадлежат сотрудники x и y. Также в запросах второго типа надо не забывать вызывать merge от всех удаляемых отрезков.
Получилось решение за время 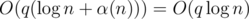 .
.
562E - Max and Min
(в трансляции: 566G - Max and Min)
Сформулируем задачу в геометрической интерпретации. У Макса и у Мина есть набор векторов из первой координатной четверти на плоскости и точка (x, y). За свой ход Макс может прибавить любой из имеющихся у него векторов к (x, y), а Мин — вычесть. Мин хочет добиться, чтобы точка (x, y) оказалась строго в третьей координатной четверти, Макс пытается ему помешать. Обозначим вектора Макса за Mxi, вектора Мина за Mnj.
Сформулируем очевидное достаточное условие для Макса, чтобы тот мог выиграть. Рассмотрим некоторое неотрицательное направление на плоскости, т. е. вектор (a, b), такой что a, b ≥ 0, при этом хотя бы одно из чисел a, b — не ноль. Тогда если среди ходов Макса есть такой вектор Mxi, что он не короче всех векторов Мина Mnj вдоль направления (a, b), то Макс может гарантировать себе победу. Здесь под длиной вектора v вдоль направления (a, b) подразумевается скалярное произведение вектора v на вектор (a, b).
Действительно, пусть Макс постоянно ходит в этот вектор Mxi. Тогда за пару ходов Макса и Мина точка (x, y) сдвинется на вектор Mxi - Mnj для некоторого j, а значит её сдвиг вдоль вектора (a, b) составит ((Mxi - Mnj), (a, b)) = (Mxi, (a, b)) - (Mnj, (a, b)) ≥ 0. Значит, так как исходно скалярное произведение ((x, y), (a, b)) = ax + by > 0, то и в любой момент времени ax + by будет строго положительно. А значит, Мин ни в какой момент времени не сможет добиться чтобы x и y стали оба отрицательными (так как это значило бы, что ax + by < 0).
Теперь сформулируем некоторый вариант обратного утверждения. Пусть вектор Макса Mxi лежит строго внутри треугольника, образованного векторами Мина Mnj и Mnk. При этом, вектор Mxi не может лежать на отрезке [Mnj, Mnk], но может быть коллинеарен одному из векторов Mnj и Mnk.
Заметим, что раз Mxi лежит строго внутри треугольника, натянутого на Mnj и Mnk, то его можно продлить до вектора Mx'i, конец которого лежит на отрезке [Mnj, Mnk]. В силу линейной зависимости Mx'i и Mnj, Mnk, имеем, что Mx'i = (p / r)Mnj + (q / r)Mnk, где p + q = r и p, q, r — целые неотрицательные числа. Это эквивалентно rMx'i = pMnj + qMnk, а значит, если на каждые r ходов Макса в Mxi мы будем отвечать p ходами Мина в Mnj и q ходами Мина в Mnk, то суммарный сдвиг составит - pMnj - qMnk + rMxi = - rMx'i + rMxi = - r(Mx'i - Mxi), то есть вектор со строго отрицательными компонентами. Таким образом, мы можем мажорировать данный ход Макса, т. е. он ему невыгоден.
Естественным образом возникает желание построить выпуклую оболочку на ходах Мина и посмотреть на все ходы Макса относительно неё. Если ход Макса лежит внутри выпуклой оболочки ходов Мина, то из предыдущего утверждения этот ход Максу невыгоден. В противном случае, возможно два варианта.
Либо этот ход пересекает выпуклую оболочку, но выходит из неё наружу — в таком случае этот ход Макса не короче всех ходов Мина в некотором неотрицательном направлении, а значит Макс победил.
Либо же, вектор Макса находится сбоку от выпуклой оболочки ходов Мина. Пусть для определённости вектор Mxi В таком случае, требуется отдельный анализ. Рассмотрим самый верхний из векторов Мина. Если вектор Mxi не ниже самого верхнего из ходов Макса Mxj, то по первому утверждению Макс может выиграть, ходя исключительно в этот вектор. В противном же случае, как несложно видеть, разность Mni - Mxj — это вектор со строго отрицательными компонентами, ходя в который мы можем мажорировать соответствующий вектор Макса.
Значит, полная версия критерия победы Мина выглядит следующим образом. Рассмотрим выпуклую оболочку ходов Мина и продлим её от самой верхней точки влево и от самой правой точки вниз. Если все ходы Макса попадают строго внутрь образованной фигуры, то Мин побеждает. Иначе побеждает Макс.
562F - Matching Names
Сформиурем бор из всех имён и псевдонимов. Отметим красным все вершины, соответствующие именам, и синим все вершины, соответствующие всем псевдонимам (одна вершина может быть отмечена несколько раз, в том числе разными цветами). Заметим, что если мы сопоставили имя a и псевдоним b, то качество такого сопоставления может быть выражено как lcp(a, b) = 1 / 2(2 * lcp(a, b)) = 1 / 2(|a| + |b| - (|a| - lcp(a, b)) - (|b| - lcp(a, b))), что представляет собой константу 1 / 2(|a| + |b|), из которой вычитается половина длины пути между a и b по бору. Таким образом, мы должны соединить все красные вершины с синими, минимизировав суммарную длину путей.
Нетрудно видеть, что такая задача решается жадным образом следующей рекурсивной процедурой: если у нас есть вершина v, в поддереве которой x красных вершин и y синих вершин, то мы должны сопоставить min(x, y) красных вершин этого поддерева синим вершинам, а оставшиеся max(x, y) - min(x, y) красных или синих вершин "отдать" на уровень выше. Корректность данного алгоритма легко объясняется следующим соображением. Ориентируем ребро каждого пути по направлению от красной вершины к синей. Если ребро получает две разных ориентации, то два пути, на которых оно лежит, легко "развести", уменьшив их суммарную длину.
Таким образом, получается несложное решение за O(sumlen), где sumlen — суммарная длина всех имён и псевдонимов.
(в трансляции: 566A - Matching Names)
562G - Replicating Processes
(в трансляции: 566B - Replicating Processes)
Эту задачу можно решить симулируя процесс реплицирования. Будем к каждому шагу поддерживать список всех репликаций, которые в текущий момент можно применить. Применяем любую репликацию, после чего обновляем список, добавляя/удаляя все подходящие или переставшие быть подходящими репликации со всех затронутых на данном шаге серверов. Список репликаций можно поддерживать в структуре данных "двусвязный список", которая позволяет за O(1) добавлять и удалять элемент в/из множества и вынимаь произвольный элемент множества.
Доказательство корректности этого алгоритма несложно и оставляется как упражнение (впрочем, если будет большое количество желающих, оно появится здесь позднее).
Получается решение за O(n) операций (впрочем, константа, скрытая за O-нотацией весьма немаленькая — один только ввод составляет 12n чисел, да и само решение оперирует по меньшей мере константой 36).







