Cutting to the chase

“Why not logarithm my problems?” you might ask. My answer will be: you can't always do that.

It has been written about sqrt decomposition many times. Still, many people see as a poor cousin of segment trees or as the crippled child of data structures. There are a lot of tutorials on the topic, but I'll try my best to offer a different perspective and bust the segment tree supremacy by giving this little kid a flamethrower.

Basics

You are given an array of length n. Answer to m query of types:

1. “What is the maximum element in interval [x,y] ? ”.
2. The elements on position x take the value y.

The brute force goes like that: we shall iterate from x to y for each query and compute the answer. The update will be O(1) and query O(N). That is O(N*M).

The key element in sqrt decomposition is skipping. Let's define a k-segment as a continuous subsequence from an array that has the length less or equal to k. We shall divide our array in as little k-segments as possible. For example array [1,2,3,4,5,6,7,8,9,10,11,12,13] divided in 3-segments looks like: [1,2,3] [4,5,6] [7,8,9] [10,11,12] [13]. Note that this greedy split of adding elements to a segment if possible ensures us with a maximum number of k-segments.

Now let's apply the k-segment concept to our queries. Let's say we want to find the maximum on interval [3,11]. That is find the maximum out of elements 3] [4,5,6] [7,8,9] [10,11. Let's observe we have “full” and “broken” 3-segments in our example. What is the maximum number of “broken” segments ? It's two ( the left and right border segments ).

Finally , having all this stuff sorted out , I'll present you the final solution.

We record for each segment it's elements and the maximum element. An update is made by replacing the element on the x-th position and updating the maximum on the k-segment. A query can be responded by calculating the maximum on “broken” k-segments and the maximum of the values of the “full” segments.

The complexity is O(K) for an update , O(K+N/K) for a query and O(N) for building the structure. If we take K = sqrt(N) , then the complexity will be O(N+M sqrt N).

Here is an (object oriented) approach to implement the problem above.

You can also read more about the basics (and other stuff) here.

Replacing lazy deletion

You are given an array of length n. Answer to m query of types:

1. “What is the maximum element in interval [x,y] ? ”.
2. The elements on positions [x,y] take the value z.

The only thing we must keep in addition is a variable ff that works as follows:

• if ff != 0 then the maximum will be fixed
• if ff == 0 then we have to compute the maximum

It works just as lazy deletion on segment trees. That is, if we need to look for a value inside a k-segment then is the segment is fixed we update all it's elements with ff. If we need to compute the maximum on a fixed segment is not necessary to go inside it, but rather just respond with value ff. Complexity will be O(N+M sqrt N).

Why the k-segment notation ?

Sometimes taking K=sqrt(N) isn't the best idea. It was the case the following problem form National Olympics in Informatics Romania.

We have a vector v with n elements and a number m. The vector has to be split in exactly m continuous subsequences such that each element has to be in one subsequence. We define the control value of some subsequence as [(maximum-minimum+1)/2]. We have to split the array such that the maximum control value of each subsequence will be as small as possible. ( n <= 1,000,000 and m <= 1000 )

For example if we split the array [13,4,6,19,4,10] in [13,4,6] , [19] , [4,10] we have the control values 5,0,3 so the answer will be 5.

Firstly , let's solve the problem in a not-so-good complexity. We binary search the result, making a greedy verification function. As long as one can expand the current continuous sequence to the right side ( i.e. [(maximum-minimum+1)/2] <= binary_searched_value ) , we move to the right. If we can split the array in m or less sequences, the verification function will return true. The complexity will be O(N log max_ans).

Now we have to improve the complexity of some verification. We split the array in k-sequences ( of length k ). For each sequence keep maximum and minimum. Now, instead of trying to add only one value to the sequence we can try to add k values to it. This will give us the complexity O(N/K+M*K) per verification as we have maximum N/K “full” k-segments to be added and we start to add a new continuous segment to the solution at most M times.

The only thing lest to do it to choose K. If we choose K = sqrt(N) ( <= M ), this will give no improvement. But if we choose K as 100 , this will make our algorithm significantly faster. Final complexity will be O(N + (N/K+M*K) log max_ans).

Give that kid a flamethrower

Now were talking business, right ?

1. Conex graph

You are given a conex graph with n nodes and m edges. You are given q queries of the type k , a[1] , a[2] … a[k] ( 1 <= a[i] <= m ) and you have to find out for each query if the graph is conex after eliminating edges with indexes a[1] , a[2] … a[k]. Note that each query is independent. ( q*k , m <= 100,000 )

The solution that uses sqrt decomposition splits the queries in groups of k = sqrt(q). Now let's solve the problem for each group of queries.

First of all , let's compress all the nodes that we are not interested in. That is we keep all edges instead of edges in all queries in the current bunch and make a new node for each conex component in this graph. The new graph will have only nodes and no edges.

Let's compute the answer for each query in our bunch. For a query we will add edges in the new graph. Each added edge has a corresponding edge in the old graph. The edges in the old graph that I referred to are all groups of edges for all other k-1 queries.

The complexity will be O(N+sqrt(Q)*K) per bunch. In total the complexity will be O(sqrt(Q) * (N+sqrt(Q)*K)) = O(N*sqrt(Q)+Q*K).

To be sure you understood, let's take a quick example. In the picture the edges marked with red are the first query and the ones with blue are the second one. Suppose we make a bunch out of queries 1 and 2.

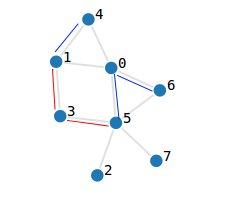
The new graph will be made out of nodes 0' = [0,1,4] , 1' = [3] , 2' = [2,5,6,7]. When we solve query one, edges (1,4) , (0,5) , (0,6) will be added, so in the new graph we will have an edge added between 0' and 2' , therefore the new graph will not be conex. When we solve query two, edges (1,3) , (3,5) are added, so (0',1') and (1',2') are added in the new graph, therefore the new graph will be conex.