Hints:
div2A: Try conversions between bases.
div2B: Solve a simpler version of the problem where Ai + 1 ≠ Ai for all i.
div1A: What are the shortest paths of the vehicles? what's the shorter of those paths?
div1B: Forget about the ceiling function. Draw points (i, A[i]) and lines between them — what's the Lipschitz constant geometrically?
div1C: Some dynamic programming. Definitely not for the exp. score of one person — look at fixed scores instead.
div1D: Compute dif(v) in O(N) (without hashing) and then solve the problem in O(N2). You need some smart merges.
div1E: Can you solve the problem without events of type 1 or 2? Also, how about solving it offline — as queries on subsets.

Div. 2 A: Two Bases
It's easy to compare two numbers if the same base belong to both. And our numbers can be converted to a common base — just use the formulas
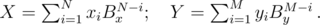
A straightforward implementation takes O(N + M) time and memory. Watch out, you need 64-bit integers! And don't use pow — iterating 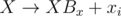 is better.
is better.
Div. 2 B: Approximating a Constant Range
Let's process the numbers from left to right and recompute the longest range ending at the currently processed number.
One option would be remembering the last position of each integer using STL map<>/set<> data structures, looking at the first occurrences of Ai plus/minus 1 or 2 to the left of the current Ai and deciding on the almost constant range ending at Ai based on the second closest of those numbers.
However, there's a simpler and more efficient option — notice that if we look at non-zero differences in any almost constant range, then they must alternate: .., + 1, - 1, + 1, - 1, ... If there were two successive differences of + 1-s or - 1-s (possibly separated by some differences of 0), then we'd have numbers a - 1, a, a, ..., a, a + 1, so a range that contains them isn't almost constant.
Let's remember the latest non-zero difference (whether it was +1 or -1 and where it happened); it's easy to update this info when encountering a new non-zero difference.
When doing that update, we should also check whether the new non-zero difference is the same as the latest one (if Ai - Ai - 1 = Aj + 1 - Aj). If it is, then we know that any almost constant range that contains Ai can't contain Aj. Therefore, we can keep the current leftmost endpoint l of a constant range and update it to j + 1 in any such situation; the length of the longest almost constant range ending at Ai will be i - l + 1.
This only needs a constant number of operations per each Ai, so the time complexity is O(N). Memory: O(N), but it can be implemented in O(1).
Bonus: the maximum difference permitted in an almost constant range is an arbitrary D.

Div. 2 C / Div. 1 A: The Two Routes
The condition that the train and bus can't meet at one vertex except the final one is just trolling. If there's a railway  , then the train can take it and wait in town N. If there's no such railway, then there's a road
, then the train can take it and wait in town N. If there's no such railway, then there's a road  , the bus can take it and wait in N instead. There's nothing forbidding this :D.
, the bus can take it and wait in N instead. There's nothing forbidding this :D.
The route of one vehicle is clear. How about the other one? Well, it can move as it wants, so the answer is the length of its shortest path from 1 to N... or - 1 if no such path exists. It can be found by BFS in time O(N + M) = O(N2).
In order to avoid casework, we can just compute the answer as the maximum of the train's and the bus's shortest distance from 1 to N. That way, we compute 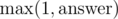 ; since the answer is ≥ 1, it works well.
; since the answer is ≥ 1, it works well.
In summary, time and memory complexity: O(N2).
Bonus: Assume that there are M1 roads and M2 railways given on the input, all of them pairwise distinct.
Bonus 2: Additionally, assume that the edges are weighted. The speed of both vehicles is still the same — traversing an edge of length l takes l hours.
Div. 2 D / Div. 1 B: Lipshitz Sequence
Let 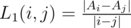 for i ≠ j.
for i ≠ j.
Key observation: it's sufficient to consider j = i + 1 when calculating the Lipschitz constant. It can be seen if you draw points (i, Ai) and lines between them on paper — the steepest lines must be between adjacent pairs of points.
In order to prove it properly, we'll consider three numbers Ai, Aj, Ak (i < j < k) and show that one of the numbers L1(i, j), L1(j, k) is ≥ L1(i, k). W.l.o.g., we may assume Ai ≤ Ak. There are 3 cases depending on the position of Aj relative to Ai, Ak:
Aj > Ai, Ak — we can see that L1(i, j) > L1(i, k), since |Aj - Ai| = Aj - Ai > Ak - Ai = |Ak - Ai| and j - i < k - i; we just need to divide those inequalities
Aj < Ai, Ak — this is similar to the previous case, we can prove that L1(j, k) > L1(i, k) in the same way
Ai ≤ Aj ≤ Ak — this case requires more work:
- we'll denote d1y = Aj - Ai, d2y = Ak - Aj, d1x = j - i, d2x = k - j
- then, L1(i, j) = d1y / d1x, L1(j, k) = d2y / d2x, L1(i, k) = (d1y + d2y) / (d1x + d2x)
- let's prove it by contradiction: assume that L1(i, j), L1(j, k) < L1(i, k)
- d1y + d2y = L1(i, j)d1x + L1(j, k)d2x < L1(i, k)d1x + L1(i, k)d2x = L1(i, k)(d1x + d2x) = d1y + d2y, which is a contradiction
We've just proved that to any L1 computed for two elements A[i], A[k] with k > i + 1, we can replace one of i, j by a point j between them without decreasing L1; a sufficient amount of such operations will give us k = i + 1. Therefore, the max. L1 can be found by only considering differences between adjacent points.
This is actually a huge simplification — the Lipschitz constant of an array is the maximum abs. difference of adjacent elements! If we replace the array A[1..n] by an array D[1..n - 1] of differences, D[i] = A[i + 1] - A[i], then the Lipschitz constant of a subarray A[l, r] is the max. element in the subarray D[l..r - 1]. Finding subarray maxima actually sounds quite standard, doesn't it?
No segment trees, of course — there are still too many subarrays to consider.
So, what do we do next? There are queries to answer, but not too many of them, so we can process each of them in O(N) time. One approach that works is assigning a max. difference D[i] to each subarray — since there can be multiple max. D[i], let's take the leftmost one.
We can invert it to determine the subarrays for which a given D[i] is maximum: if D[ai] is the closest difference to the left of D[i] that's ≥ D[i] or ai = 0 if there's none, and D[bi] is the closest difference to the right that's > D[i] or bi = n - 1 if there's none (note the strict/non-strict inequality signs — we don't care about differences equal to D[i] to its right, but there can't be any to its left, or it wouldn't be the leftmost max.), then those are all subarrays D[j..k] such that ai < j ≤ i ≤ k < bi.
If we don't have the whole array D[1..n - 1], but only some subarray D[l..r], then we can simply replace ai by 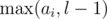 and bi by
and bi by 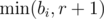 . The number of those subarrays is Pi = (i - ai)(bi - i), since we can choose j and k independently.
. The number of those subarrays is Pi = (i - ai)(bi - i), since we can choose j and k independently.
All we have to do to answer a query is check all differences, take ai, bi (as the max/min with some precomputed values) and compute Pi; the answer to the query is 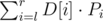 . We only need to precompute all ai, bi for the whole array D[1..n - 1] now; that's a standard problem, solvable using stacks in O(N) time or using maps + Fenwick trees in
. We only need to precompute all ai, bi for the whole array D[1..n - 1] now; that's a standard problem, solvable using stacks in O(N) time or using maps + Fenwick trees in 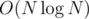 time.
time.
The total time complexity is O(NQ), memory O(N).
Bonus: Q ≤ 105.

Div. 1 C: Kleofáš and the n-thlon
As it usually happens with computing expected values, the solution is dynamic programming. There are 2 things we could try to compute: probabilities of individual overall ranks of Kleofáš or just some expected values. In this case, the latter option works.
- "one bit is 8 bytes?"
- "no, the other way around"
- "so 8 bytes is 1 bit?"
After some attempts, one finds out that there's no reasonable way to make a DP for an expected rank or score of one person (or multiple people). What does work, and will be the basis of our solution, is the exact opposite: we can compute the expected number of people with a given score. The most obvious DP for it would compute E(i, s) — the exp. number of people other than Kleofáš with score s after the first i competitions.
Initially, E(0, 0) = m - 1 and E(0, s > 0) = 0. How can we get someone with score s in competition i? That person can have any score k from 1 to m except xi (since Kleofáš has that one) with the same probability 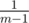 . The expected values are sums with probabilities P(i, s, j) that there are j people with score s:
. The expected values are sums with probabilities P(i, s, j) that there are j people with score s:
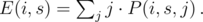
Considering that the probability that one of them will get score k is  , we know that with probability
, we know that with probability 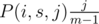 , we had j people with score s before the competition and one of them had score s + k after that competition — adding 1 to E(i + 1, s + k). By summation over j, we'll find the exp. number of people who had overall score s and scored k more:
, we had j people with score s before the competition and one of them had score s + k after that competition — adding 1 to E(i + 1, s + k). By summation over j, we'll find the exp. number of people who had overall score s and scored k more:
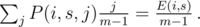
Lol, it turns out to be so simple.
We can find the probability E(i + 1, t) afterwards: since getting overall score t after i + 1 competitions means getting score k in the currently processed competition and overall score s = t - k before, and both distinct k and expectations for people with distinct s are totally independent of each other, then we just need to sum up the exp. numbers of people with those scores (which we just computed) over the allowed k:
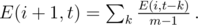
The formulas for our DP are now complete and we can use them to compute E(n, s) for all 1 ≤ s ≤ mn. Since E(n, s) people with s greater than the overall score sk of Kleofáš add E(n, s) to the overall rank of Kleofáš and people with s ≤ sk add nothing, we can find the answer as
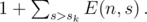
This takes O(m2n2) time, since there are O(mn) scores, O(mn2) states of the DP and directly computing each of them takes O(m) time. Too slow.
We can do better, of course. Let's forget about dividing by m - 1 for a while; then, E(i + 1, t) is a sum of E(i, s) for one or two ranges of scores — or for one range minus one value. If you can solve div1C, then you should immediately know what to do: compute prefix sums of E(i, s) over s and find E(i + 1, t) for each t using them.
And now, computing one state takes O(1) time and the problem is solved in O(mn2) time (and memory).
Bonus: Really, how fast can you solve this problem?

Div. 1 D: Acyclic Organic Compounds
The name is really almost unrelated — it's just what a tree with arbitrary letters typically is in chemistry.
If you solved problem TREEPATH from the recent Codechef November Challenge, this problem should be easier for you — it uses the same technique, after all.
Let's figure out how to compute 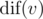 for just one fixed v. One more or less obvious way is computing hashes of our strings in a DFS and then counting the number of distinct hashes (which is why there are anti-hash tests :D). However, there's another, deterministic and faster way.
for just one fixed v. One more or less obvious way is computing hashes of our strings in a DFS and then counting the number of distinct hashes (which is why there are anti-hash tests :D). However, there's another, deterministic and faster way.
Compressing the subtree Tv into a trie.
Recall that a trie is a rooted tree with a letter in each vertex (or possibly nothing in the root), where each vertex encodes a unique string read along the path from the root to it; it has at most σ sons, where σ = 26 is the size of the alphabet, and each son contains a different letter. Adding a son is done trivially in O(σ) (each vertex contains an array of 26 links to — possibly non-existent — sons) and moving down to a son with the character c is then possible in O(1).
Compressing a subtree can be done in a DFS. Let's build a trie Hv (because Tv is already used), initially consisting only of one vertex — the root containing the letter sv. In the DFS, we'll remember the current vertex R of the tree T and the current vertex cur of the trie. We'll start the DFS at v with cur being the root of Hv; all we need to do is look at each son S of R in DFS, create the son curs of cur corresponding to the character sS (if it didn't exist yet) and run DFS(S, curs). This DFS does nothing but construct Hv that encodes all strings read down from v in Tv. And since each vertex of Hv encodes a distinct string, 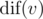 is the number of vertices of Hv.
is the number of vertices of Hv.
This runs in O(|Tv|σ) time, since it can create a trie with |Tv| vertices in the worst case. Overall, it'd be O(N2σ) if T looks sufficiently like a path.
The HLD trick
Well, what can we do to improve it? This trick is really the same — find the son w of v that has the maximum |Tw|, add sv to Hw and make it Hv; then, DFS through the rest of Tv and complete the trie Hv as in the slow solution. The trick resembles HLD a lot, since we're basically remembering tries on HLD-paths.
If v is a leaf, of course, we can just create Hv that consists of one vertex.
How do we "add" v to a trie Hw of its son w? Well, v should be the root of the trie afterwards and the original Hw's root should become its son, so we're rerooting Hw. We'll just create a new vertex in Hw with sv in it, make it the root of Hw and make the previous root of Hw its son. And if we number the tries somehow, then we can just set the number of Hv to be the number of Hw.
It remains true that dif(v) is |Hv| — the number of vertices in the trie Hv, which allows us to compute those values directly. After computing dif(v) for each v, we can just compute both statistics directly in O(N).
Since each vertex of T corresponds to vertices in at most 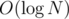 tries (for each heavy edge that's on the path from it to the root), we aren't creating tries with a total of O(N2) vertices, but
tries (for each heavy edge that's on the path from it to the root), we aren't creating tries with a total of O(N2) vertices, but 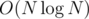 . The time complexity is therefore
. The time complexity is therefore  . However, the same is true for the memory, so you can't waste it too much!
. However, the same is true for the memory, so you can't waste it too much!
Bonus: you have an additional tiebreaker condition for vertices with identical  . Count the number of distinct strings which occurred exactly k times for each k in an array Pr[]; take the vertex/vertices with lexicograhically maximum Pr[] (as many strings as possible which occur only once, etc).
. Count the number of distinct strings which occurred exactly k times for each k in an array Pr[]; take the vertex/vertices with lexicograhically maximum Pr[] (as many strings as possible which occur only once, etc).
Bonus 2: Can you get rid of the logarithm in the time complexity?

Comic strip name: Indy. Go read the whole thing, it's not very long, but pretty good.
Div. 1 E: A Museum Robbery
In this problem, we are supposed to solve the 0-1 knapsack problem for a set of items which changes over time. We'll solve it offline — each query (event of type 3) is asked about a subset of all N exhibits appearing on the input.
Introduction
If we just had 1 query and nothing else, it's just standard knapsack DP. We'll add the exhibits one by one and update s(m) (initially, s(m) = 0 for all m). When processing an exhibit with (v, w), in order to get loot with mass m, we can either take that exhibit and get value at least s(m - w) + v, or not take it and get s(m); therefore, we need to replace s(m) by  ; the right way to do it is in decreasing order of m.
; the right way to do it is in decreasing order of m.
In fact, it's possible to merge 2 knapsacks with any number of items in O(k2), but that's not what we want here.
Note that we can add exhibits this way. Thus, if there were no queries of type 2, we would be able to solve whole problem in O(Nk) time by just remembering the current s(m) and updating it when adding an exhibit. Even if all queries were of type 2 (with larger n), we'd be able to solve it in O(nk) time in a similar way after sorting the exhibits in the order of their removal and processing queries/removals in reverse chronological order.
The key
Let's have q queries numbered 1 through Q in the order in which they're asked; query q is asked on some subset Sq of exhibits.
MAGIC TRICK: Compute the values s(m) only for subsets  — the intersections of pairs of queries 2q, 2q + 1 (intersection of the first and the second query, of the third and fourth etc.), recursively. Then, recompute s(m) for all individual queries in O((N + Q)k) time by adding elements which are missing in the intersection, using the standard knapsack method.
— the intersections of pairs of queries 2q, 2q + 1 (intersection of the first and the second query, of the third and fourth etc.), recursively. Then, recompute s(m) for all individual queries in O((N + Q)k) time by adding elements which are missing in the intersection, using the standard knapsack method.
What?! How does this work?! Shouldn't it be more like O(N2) time? Well, no — just look at one exhibit and the queries where it appears. It'll be a contiguous range of them — since it's displayed until it's removed (or the events end). This element will only be missing in the intersection, but present in one query (so it'll be one of the elements added using knapsack DP), if query 2q + 1 is the one where it appears first or query 2q the one where it appears last. That makes at most two addittions of each element and O(N) over all of them; adding each of them takes O(k) time, which gives O(Nk).
The second part of the complexity, O(Qk) time, is spent by copying the values of s(m) first from the intersection of queries 2q and 2q + 1 to those individual queries.
If we're left with just one query, we can solve it in O(Nk) as the usual 0-1 knapsack.
Since we're halving the number of queries when recursing deeper, we can only recurse to depth 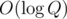 and the time complexity is
and the time complexity is 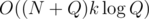 .
.
A different point of view (Baklazan's)
We can also look at this as building a perfect binary tree with sets S1, ..., SQ in leaves and the intersection of sets of children in every other vertex.
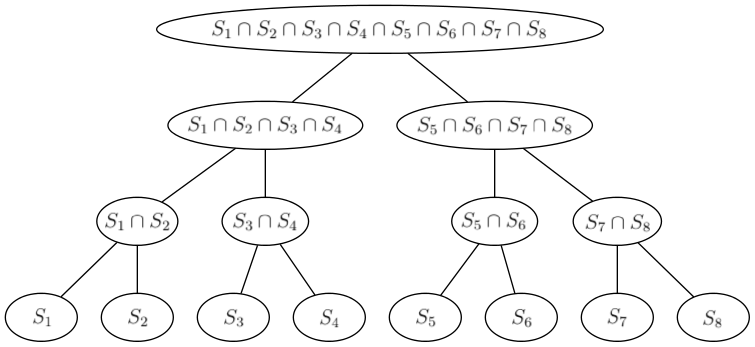
For each vertex v of this tree, we're solving the knapsack — computing s(m) — for the set Dv of displayed exhibits in it. We will solve the knapsack for the root directly and then proceed to the leaves. In each vertex v, we will take s(m), the set Dp of its parent p and find s(m) for v by adding exhibits which are in Dv, but not in Dp.
We know that the set Dp is of the form 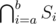 for some a, b and Dv is either of the form
for some a, b and Dv is either of the form  or
or 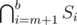 for
for 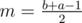 (depending on whether it's the left or the right son). In the first case, only elements removed between the m-th and b-th query have to be added and in the second case, it's only elements added between the a-th and m + 1-th query. Since each element will only be added/removed once and the ranges of queries on the same level of the tree are disjoint, we will do O((N + Q)k) work on each level and the overall time complexity is
(depending on whether it's the left or the right son). In the first case, only elements removed between the m-th and b-th query have to be added and in the second case, it's only elements added between the a-th and m + 1-th query. Since each element will only be added/removed once and the ranges of queries on the same level of the tree are disjoint, we will do O((N + Q)k) work on each level and the overall time complexity is 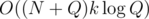 .
.
Finding the intersections and exhibits not in the intersections
Of course, bruteforcing them in O(NQ) isn't such a bad idea, but it'd probably TLE — and we can do better. We've just described how we can pick those exhibits based on the queries between which they were added/removed. Therefore, we can find — for each exhibit — the interval of queries for which it was displayed and remember for each two consecutive queries the elements added and removed between them; finding the exhibits added/removed in some range is then just a matter of iterating over them. Since we're actually adding all of them, this won't worsen the time complexity.
In order to efficiently determine the exhibits in some set 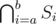 , we can remember for each exhibit the interval of time when it was displayed. The exhibit is in the set
, we can remember for each exhibit the interval of time when it was displayed. The exhibit is in the set 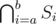 if and only if it was displayed before the a-th query and remained displayed at least until the b-th query.
if and only if it was displayed before the a-th query and remained displayed at least until the b-th query.
To conclude, the time complexity is 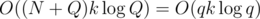 and since we don't need to remember all levels of the perfect binary tree, but just the one we're computing and the one above it, the memory complexity is O(qk).
and since we don't need to remember all levels of the perfect binary tree, but just the one we're computing and the one above it, the memory complexity is O(qk).






