Block Tree
Story
I was trying to solve this problem from the gym and I struggled to find the solution. Finally, I came up with a very interesting data structure capable of handling any subtree update and really don't know if someone else has seen it before, but I will post it here since I could not find its name (if it has) in google. My solution was able to solve the problem with O(N) memory, O(N) in creation, 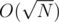 per query. When I saw the editorial I saw that it had another interesting approach with an update buffer which solved the problem in
per query. When I saw the editorial I saw that it had another interesting approach with an update buffer which solved the problem in 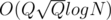 , for my surprise my solution was
, for my surprise my solution was 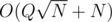 summing the creation and queries, and I saw conveniently the author used Q < = 104 so probably the author didn't know about my approach.
summing the creation and queries, and I saw conveniently the author used Q < = 104 so probably the author didn't know about my approach.
After analyzing my approach and reading one of the comments in the same problem, I saw that the problem could be also solvable using Square Root Decomposition in the Euler Tour Technique. Then I analyzed my approach and it seems that they are 90% the same, but the difference is in how the decomposition is stored. As some can see the relationship between KMP and AhoCorasick (Matching in Array — Matching in Tree), I see this as (Sqrt Decomposition Array — Sqrt Decomposition in a Tree). So, after posting this structure I search in what cases is my data structure better than the Euler Trick, then I thought of a new feature that can be implemented. I found it, it can dynamically change (be cut, and joined). Well, I probably have bored with this story, so let's go to the point.
Update — After posting this algorithm I received a comment with the name of this structure, it is called block-tree for those who don't know. I tried to find something on the internet but with no success.
Construction
The idea is not very hard, first do a dfs to compute subtree size and depth of each node. Order all nodes by depth in reverse order, this can be done in O(N) using counting sort. We will now create what I called fragment, we will collect small tree-like portions of the tree and assign them to fragments. The subtree size will be modified in each iteration it will count how many subtree nodes are not inside assigned to a fragment. So, each time we start with a node we shall update its subtree size, after that iterate its children again and count how many children are not assigned to a fragment, after this count reaches  , we create a special node and assign the children to this new node and remove the children from the previous parent.
, we create a special node and assign the children to this new node and remove the children from the previous parent.
for(int u : orderedNodes){
SZ[u] = 1;
for(int v : adj[u]){
SZ[u] += SZ[v];
}
newAdj = []
temp = []
spNodes = []
int sum = 0;
for(int v : adj[u]){
if( sum > sqrt(N) ){
int sp = createSpecialNode(u, temp);
spNodes.push_back(sp);
temp = [];
SZ[u] -= sum;
sum = 0;
}
}
adj[u] = concat(temp, spNodes);
}
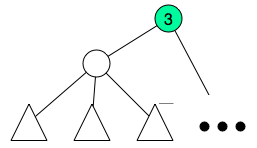
After this I will end up with  groups.
groups.
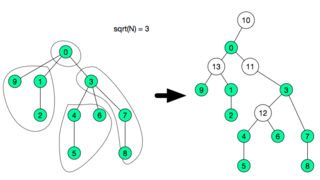
here each special node needs to be able to answer any query or update in O(1). Since the fragment is very small 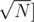 if O(1) is not possible, any other structure used in that subtree will be relatively efficient since it will be
if O(1) is not possible, any other structure used in that subtree will be relatively efficient since it will be 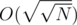 or
or  , although the time constraint will be very tight.
, although the time constraint will be very tight.
So, after this decomposition, we create a new adjacency list adjacencyList with these new nodes in O(N), and there will be  extra nodes. After that another adjacency list subAdjacencyList will be created in
extra nodes. After that another adjacency list subAdjacencyList will be created in 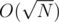 with the tree only consisting of the special nodes.
with the tree only consisting of the special nodes.
Proof of correct segmentation
I don't have a formal proof for correct segmentation, but in the construction above the ONLY way that I create a segment is only if by adding the subtree to the list it goes over  , and since the two groups of subtrees I am adding are less than
, and since the two groups of subtrees I am adding are less than  (if not they would have merged before) then each time I create a fragment it will be of size
(if not they would have merged before) then each time I create a fragment it will be of size 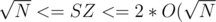 since ALL fragments have size
since ALL fragments have size 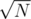 then the total number of fragments will be
then the total number of fragments will be
Unable to parse markup [type=CF_TEX]
. So segmentation is proven. If I am wrong in this informal proof, I am open to comments.Query
After the construction each query of subtree can be easily answered will be answered with a specialized dfs. The dfs will start on u and do one of two. If the node is special, then query the fragment in O(1) and recursively add the answers returned by dfs(specialChild) using the subAdjacencyList. If the node is non-special node, then apply any pending update in the fragment this node belong and query each individual node recursively using adjacencyList. It is not hard to prove that the fragment u belongs will be updated completely in  [as lazy propagation] then it will visit at most
[as lazy propagation] then it will visit at most  nodes in that same fragment and then it will query at most all the fragments. This leads to 3 time
nodes in that same fragment and then it will query at most all the fragments. This leads to 3 time  leaving a complexity of
leaving a complexity of 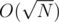 . This code is something like this:
. This code is something like this:
// G : fragment u belongs
// leader() : returns the leader of the fragment
Long getSum(int u){
if(leader(u) == u){
int fragId = fragmentOf[u];
Long w = frags[ fragId ].queryFragment();
for(int g : subAdjacencyList[ fragId ]){
w += getSum( frags[g].leader );
}
return w;
}else{
frags[ G[u] ].updateAllNodesIfPendingChanges();
Long w = u >= N ? 0 :V[ L[u] ] ;
for(int v : adjacencyList[u]){
w += getSum(v);
}
return w;
}
}
Update
If the update is in one subtree it can be done similar as the Query function with lazy updates in the fragments and active updates in  nodes. If the update is in all the nodes that are at distance L from the root (as in this problem), it is slightly different. For that we only need to iterate each fragment and update a value per level we have in that fragment (at most of size
nodes. If the update is in all the nodes that are at distance L from the root (as in this problem), it is slightly different. For that we only need to iterate each fragment and update a value per level we have in that fragment (at most of size  ) like this valueInLevel[L - leader.level] and update the value representing the whole fragment, in this case fragmentSum + = nodesInLevel[L - leader.level]. this will be done in O(1) time, for each fragment. This later update will be seen like this.
) like this valueInLevel[L - leader.level] and update the value representing the whole fragment, in this case fragmentSum + = nodesInLevel[L - leader.level]. this will be done in O(1) time, for each fragment. This later update will be seen like this.
void update(int LVL, Long v){
V[LVL] += v;
for(Fragment &f : frags){
f.update(LVL, v);
}
}
Cut/Join
Everything above is  per query, cut/join in a node is not that hard to do. For cut we will only split one fragment and add a new parentless special node. And for join we will assign a parent to that special node. This sounds as O(1), but since we need to update the old(in cut) or new(in join) parent of the cut node this will probably cost
per query, cut/join in a node is not that hard to do. For cut we will only split one fragment and add a new parentless special node. And for join we will assign a parent to that special node. This sounds as O(1), but since we need to update the old(in cut) or new(in join) parent of the cut node this will probably cost  . This sounds amazing, but there is one problem, each cut creates one special node. and the complexity of this whole structure is O(specialNodeCount) for query and update. So probably we will lose the efficiency with many cuts. To solve this, we take advantage of the O(N) creation time. Each time the whole tree has been cut
. This sounds amazing, but there is one problem, each cut creates one special node. and the complexity of this whole structure is O(specialNodeCount) for query and update. So probably we will lose the efficiency with many cuts. To solve this, we take advantage of the O(N) creation time. Each time the whole tree has been cut  times, we will rebuild the tree in O(N), so that it will recover again the optimal amount of special nodes.
times, we will rebuild the tree in O(N), so that it will recover again the optimal amount of special nodes.
Notes:
- The whole code can be seen in my submission here or here to the problem. Any tip or something wrong in this post, just leave a comment..
- Was said in comments that mugurelionut paper was the same, i thought that but then i read it carefully and they solve different problems.
- It seems there are people that knows this, waiting for some sources.






