Is there a polynomial algorithm to find a spanning tree of an undirected grid graph which minimizes the number of turns in tree? A turn is when there are two edges connected to one vertex which have perpendicular directions.
In this problem we have arbitrary set of cells in grid which form a connected graph (not only rectangles are considered). Thus, set of cells may form concave areas and areas with holes
For example, given a 4 x 4 grid graph (see image below), we want to find a spanning tree like that on the right (which has 6 turns) rather than that on the left (which has 14):
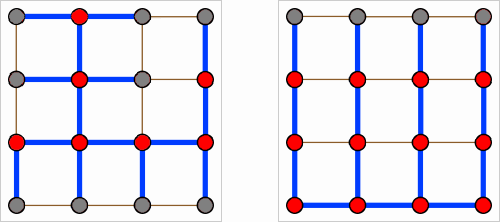
Ideas about approximate algorithms may be useful too.







