#IjustWantContribution
It seems there isn't any blog about Berlekamp-Massey Algorithm around here, so I decided to go on a try. :P
Acknowledgement: Hats off to matthew99 for introducing this algorithm.
What is 'linear recurrence'?
Assuming there is a (probably infinity) sequence a0, a1...an - 1, we call this sequence satisfies a linear recurrence relation p1, p2...pm, iff 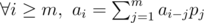 . (Obviously, if m ≥ n any p can do :P)
. (Obviously, if m ≥ n any p can do :P)
How to calculate k-th term of a linear recurrence?
For a polynomial 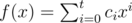 , we define
, we define 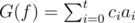 .
.
Obviously G satisfies G(f) ± G(g) = G(f ± g).
Because 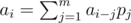 , if we let
, if we let 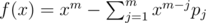 , then G(f) = 0. Also G(fx), G(fx2)... = 0. So G(fg) = 0 (g is any polynomial).
, then G(f) = 0. Also G(fx), G(fx2)... = 0. So G(fg) = 0 (g is any polynomial).
What we want is G(xk). Because G(f⌊ xk / f⌋) = 0, then 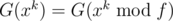 . We can calculate
. We can calculate  in a binary-exponentiation manner, then calculate
in a binary-exponentiation manner, then calculate 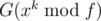 . Time complexity is
. Time complexity is 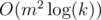 or
or 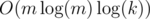 (if you use fft etc.)
(if you use fft etc.)
How to find (the shortest) linear recurrence relation?
It's Berlekamp-Massey Algorithm to the rescue! For a given sequence x0, x1...xn - 1, it can calculate one shortest linear recurrence relation for every prefix in O(n2) time.
Let's define the value of a relation sequence p1, p2...pm evaluated at position t:  (t ≥ m). A valid linear recurrence relation is a relation sequence with correct value evaluated at every position ≥ m.
(t ≥ m). A valid linear recurrence relation is a relation sequence with correct value evaluated at every position ≥ m.
Let's consider the numbers from left to right. Start from {}, we evaluate the current relation sequence at current position t (from 1 to n). If we got at, then it's still good, go on. Assume we've got value v, if we somehow got some relation sequence x that evaluated as 1 at position t, and evaluated as 0 (or undefined) at positions < t, then minus current sequence with (v - at)x, we're done.
If this is not first non-zero position, we have run into this situation before. Let's say s = {s1, s2...sm} evaluated as xt' + v' at position t' and correct at positions before t', then {1, - s1, - s2... - sm} should evaluated as v' at position t' + 1 and 0 otherwise. Divide it with v' and add proper (t - t' - 1) zeroes in front, we've got the x we need!
If we run into this situation several times before, we can choose the one that is shortest after filling zeroes.
Combine the above two section, we can acquire a handy weapon for these kind of problems :)
Because we need division, the modulus needs to be a prime.
Applications
Or, in other words, where can we find linear recurrences?
From the point of generating function, let A and P be the generating function of a and p, then A = AP + A0 (A0 depends on the first terms of a), then A = A0 / (1 - P). Moreover, if A = B / C and the constant term of C is 1 then there is a linear recurrence relation for a. So, provided with the generating function of a, one can tell if it's a linear recurrence easily.
If we have some kind of dynamic-programming f[i][j] (i ≤ n, j ≤ m), we want to find f[n][1]. The transitions of f is something like 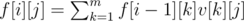 . In old days, we may use matrix-multiplications. But things have changed! Calculate f[1][1], f[2][1]...f[m + m + m][1] and plug in the above code, we're done!
. In old days, we may use matrix-multiplications. But things have changed! Calculate f[1][1], f[2][1]...f[m + m + m][1] and plug in the above code, we're done!
Why? Consider f[i] as a vector and v as a matrix, then f[i] = f[i - 1]v, so f[n] = f[1]vn - 1. Consider the minimal polynomial of v, it's degree must be ≤ m and obviously there's a corresponding linear recurrence relation with length ≤ m. With a prefix of length m + m + m it's enough to figure out a correct relation.
Why is it better than matrix multiplication? Besides it's  instead of
instead of 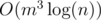 , sometimes it's hard to acquire the exact transition matrix (or maybe just you're lazy enough), and this algorithm makes life better.
, sometimes it's hard to acquire the exact transition matrix (or maybe just you're lazy enough), and this algorithm makes life better.
Try your hands
http://codeforces.com/contest/506/problem/E Write a naive dynamic-programming for small n, plug in BM, you're done! Life has never been so easy.
https://loj.ac/problem/2463 A chinese problem: Let n be a power of 2, you're given a directed graph with n nodes, from i to j there're Ai, j directed edges. Little Q is going on several trips, for every trip he will start from some node, make at least one step (i.e. go through at least one edge) and end at some node. He is wondering the number of ways if he's going on several travels, making x steps at total, and the bitwise-and of all start nodes and end nodes equals to y. For every 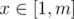 ,
, 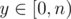 , you need to find the way modulo 998244353. To reduce output size, only output the bitwise-xor of all m × n answers. 2 ≤ n ≤ 64, 1 ≤ m ≤ 20000.
, you need to find the way modulo 998244353. To reduce output size, only output the bitwise-xor of all m × n answers. 2 ≤ n ≤ 64, 1 ≤ m ≤ 20000.
There're many more problems that can be solved in this way, but since posting them here is already spoiling I'm not going to post more :)






