Given a range (l, r) where 0.0 <= l,r <= 1.0 we want to find a fraction x/y which satisfies following condition: l <= x/y < r and y should be as small as possible. l and r might have at most 9 digits after floating point.
→ Pay attention
→ Top rated
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3880 |
| 2 | jiangly | 3669 |
| 3 | ecnerwala | 3654 |
| 4 | Benq | 3627 |
| 5 | orzdevinwang | 3612 |
| 6 | Geothermal | 3569 |
| 6 | cnnfls_csy | 3569 |
| 8 | jqdai0815 | 3532 |
| 9 | Radewoosh | 3522 |
| 10 | gyh20 | 3447 |
→ Top contributors
| # | User | Contrib. |
|---|---|---|
| 1 | awoo | 161 |
| 1 | maomao90 | 161 |
| 3 | adamant | 156 |
| 4 | maroonrk | 153 |
| 5 | -is-this-fft- | 148 |
| 5 | atcoder_official | 148 |
| 5 | SecondThread | 148 |
| 8 | Petr | 147 |
| 9 | nor | 144 |
| 10 | TheScrasse | 142 |
→ Find user
→ Recent actions
Codeforces (c) Copyright 2010-2024 Mike Mirzayanov
The only programming contests Web 2.0 platform
Server time: Jul/27/2024 03:34:22 (h2).
Desktop version, switch to mobile version.
Supported by
User lists


| Name |
|---|










Just print
((int) (l * 1000000000)) / 1000000000. If you want more precision just add zeroes.I dont really get why this gives us a fraction with smallest denumerator. Could you please explain it more?
Oops, I misread. I think this algorithm will give you smallest denominator:
Binary search on the denominator (it should never be the case that a smaller denominator works while a larger one does not, if so please tell). For every denominator, also binary search on the numerator, to try to get num/denom within [l, r). Then you can find the smallest denominator.
EDIT: Just kidding, it doesn't work
I was thinking of binary search, but is there any proof that if lets say for d1 > d2 such that for denumerator d1 is not possible, but for d2 is possible? if there is a proof, then binary search is correct. Could you please devise a proof, if you have in mind?
That is not correct. Think for example in range [0.4, 0.6]. In this case, denominator 2 works, while denominator 3 doesn't.
do you know how to solve this problem?
lets say, l = 0.115 and r = 0.125,
so we want to find a fraction which has smallest denumerator, and for this range it is 2/17. How to find 2/17 with your approach?
Is
y— must smallest as possible???Yes, in which it satisfies the condition.
see code
for for some y, it could take much more, since it is multiple test case problem.
y*r > 0 --> y*r >= 1 --> y >= 1.0 / rNote tha, binary search does not applicable there.
http://acm.timus.ru/problem.aspx?space=1&num=1011 ))
Yes seems same problem. but constraints here are small. What is the solution for this problem?
Auto comment: topic has been updated by Logarithmic (previous revision, new revision, compare).
Ok, I'm not completely sure about this approach, but here it goes. Take u = 1 / l and v = 1 / r. This are numbers bigger than one. Then, the inequality that must be satisfied is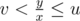 . Then,iterate through x's. Binary search for each x the value of y, and for the minimum x such that y exists, that y is your answer. According to my intuition, (sorry, I cannot offer more than that), for most cases this approach will require not more than 106 iterations or so.
. Then,iterate through x's. Binary search for each x the value of y, and for the minimum x such that y exists, that y is your answer. According to my intuition, (sorry, I cannot offer more than that), for most cases this approach will require not more than 106 iterations or so.
UPD: Sorry, it doesn't work.
Can you explain how it's only 106? Wouldn't you need to iterate over a lot more x-values, in case like [0.573529588, 0.573529590)?
Yeah, sorry, you are right.
But if there are somecases in which it takes about 10^8, then it will definitely fail, since it is multiple test case.
It seems like you could use the Stern–Brocot tree.
Start at the root. At each node, you either find the solution or have to recurse into one of the children.
If this is too slow you might be able to binary-search how far you walk down left/right before chaning to right/left to get O(log(109)2) time complexity, as the denominator grows at least as fast as the fibonacci series when alternating left/right.
Edit: One might get O(log(109)) complexity by using exponential-search instead of binary-search.
How to apply binary search here? Binary search on y seems not working :( Could you please explain it more detailed?
Can you possibly explain your binary search approach. I didn't get your idea.
I'll first explain the basic algorithm on the Stern-Brocot tree similar to here.
We start with xl = 0, yl = 1, xr = 1, yr = 1. Throughout the algorithm we keep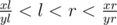 .
.
To traverse the tree we look at the middle fraction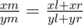 . If
. If 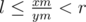 , then
, then  is the solution (Correctness follows from the properties of the Stern-Brocot tree).
is the solution (Correctness follows from the properties of the Stern-Brocot tree).
If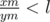 , set xl = xm, yl = ym (This is a move to the right).
, set xl = xm, yl = ym (This is a move to the right).
If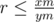 , set xr = xm, xr = ym (This is a move to the left).
, set xr = xm, xr = ym (This is a move to the left).
The above algorithm takes a long time if we keep moving the same direction over and over.
What we can do, is move k times to the left by setting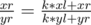 and similarily for moving to the right.
and similarily for moving to the right.
The faster algorithm now works as follows: When moving into a certain direction, binary-search for the value of k — how far the slow algorithm would move into that direction before changing directions. Then move k steps into that direction.
Edit: Fixed some small things.
Edit2:
For a given ymax, let's ask how many valid fractions with y ≤ ymax there are. For chosen y, the number of valid x's is ⌊ ry⌋ - ⌊ ly⌋. So the total number of valid fractions is:
Now, note that we can express l as a fraction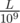 , where L is an integer. Same with r. It's possible to calculate the sum
, where L is an integer. Same with r. It's possible to calculate the sum 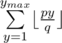 quickly using this algorithm. Once we can find it, we can do a binary search on that value, and the result will be the smallest ymax that produces a non-zero result.
quickly using this algorithm. Once we can find it, we can do a binary search on that value, and the result will be the smallest ymax that produces a non-zero result.
Thanks for the solution. One more point, it should be strictly less than r. how to exclude that? is the only way just to replace r with some r-eps?
I would subtract the number of x = ry from the result (and add the number of x = ly because the other inequality is ≤ ). If where p,q are coprime, then a valid (x, y) pair is in the form (kp, kq) with k integer, so there are
where p,q are coprime, then a valid (x, y) pair is in the form (kp, kq) with k integer, so there are  such points.
such points.
Yes, it will work, thanks for the help
Let me show a test which your formula gives wrong answer:
l = 0.125 and r = 0.130your formula gives4 / 31, but correct answer is1/8.Without the clarification I made in my other comment above it is indeed incorrect. You need to add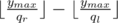 , where qr and ql are denominators of
, where qr and ql are denominators of 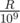 and
and 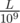 respectively, after simplifying the fractions (qr = 100 and ql = 8 in your case).
respectively, after simplifying the fractions (qr = 100 and ql = 8 in your case).
Thx, now understand.
your link not worked for me, can share another link ?
Did you try adding www or http to the beginning of the address? The outline of the idea is:
Let's take a sum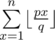 with p and q coprime. If n ≥ q or p > q, they can be reduced to n mod q (since
with p and q coprime. If n ≥ q or p > q, they can be reduced to n mod q (since 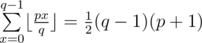 ) and p mod q (since
) and p mod q (since 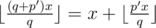 ) by adding a constant. Now, let
) by adding a constant. Now, let 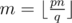 . After a few transformations we can get
. After a few transformations we can get 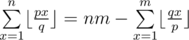 . Since p < q, we can again reduce q to q mod p and so on. The reductions structure will be the same as gcd calculation, and a single step will take constant time, giving overall O(log(p)+log(q)) complexity.
. Since p < q, we can again reduce q to q mod p and so on. The reductions structure will be the same as gcd calculation, and a single step will take constant time, giving overall O(log(p)+log(q)) complexity.
The last formula only holds when xq/p is never an integer for x from 1 to m. I think this can happen from time to time.
After the first two steps, we have that n < q, p ≤ q. Hence m < p. As p and q are coprime, p divides xq if and only if p divides x. But 0 < x ≤ m < p contradiction. Hence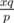 is never an integer.
is never an integer.
(And the post you replied to was 2 years old.)
Yes, you are right. I was think of the situation when n is greater than q.
(aren't you curious why you get 10 thumbs up under a blog that is 2 years old?)
Auto comment: topic has been updated by Logarithmic (previous revision, new revision, compare).