(a/b) (mod P) = (a * b^-1) (mod P) = (a (mod P) * b^-1 (mod P)) (mod P).
Now, by Fermat's theorem, b-1 (mod P) will be b^P-2 (mod P). Of course, for this b and P must be co-prime to each other and P must be a prime. So, (a/b) (mod P) = (a (mod P) * b^P-2 (mod P)) (mod P). works only if P is prime and a,b are coprime to P










If P prime you can use fermat Dont depend on a,b. Also you can use fucntion of the Euler. a/b mod P = a * b^(f(P)) mod P. f — Euler fucn. For prime num f(p)=p-2.
There is a small mistake in your explanation. Actually, you need to multiply A by B in power of f(P)-1 and f(P) for prime number is P-1.
Sorry. You are right, i forgot about it.
NO You are wrong!!!!!! very bad .. don't mislead
You can also use extended euclid if a and P are coprime. Here's the equation a'x + b'y = gcd(a', b'), put a' = b and b' = P, since gcd(a, P) = 1, taking modulo both sides you have x as your answer.
If b | a, then we can do some thing like: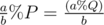 , Where Q = P * b.
, Where Q = P * b.
I think your idea is quite wonderful. I have met a problem asking, for instance, to calculate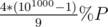 , and I think your idea can solve this sort of problem very well.
, and I think your idea can solve this sort of problem very well.
Perhaps it is even not necessary for P to be a prime integer under this condition.
Yes, it's good idea when b is small, but when it's big, this formula become not practical at all.
Great Idea! In a problem, I was told to find (1 + a2 + a3 + ... + ab - 1)modN .It seems I can now use the Geometric Sum Formula.
What should i do when p is not prime And a,b are not co-prime to p?
Let's talk about the question when p is prime but a, b are not co-prime to p factorize the power of $$$p$$$ from $$$a (a_p)$$$ and $$$b (b_p)$$$
the answer is $$$\frac{a}{p^{a_p}} \div \frac{b}{p^{b_p}} \times p^{a_p-b_p}$$$
in this case $$$\frac{a}{p^{a_p}}$$$ and $$$\frac{b}{p^{b_p}}$$$ are both coprime. Therefore, there won't be any problem calculating the modular inverse
However this approach is basically useless unless $$$a$$$ is within 64-bit integer range.
One special usage of this is extended lucas theorem
Now, lets talk about scenarios when p is not a prime
We know that $$$p$$$ can be expressed as the product of prime powers
$$$p = P_1^{C_1} P_2^{C_2} ... P_K^{C_K}$$$
after that we can solve each $$$P_i$$$ using the above method and merge the result using Chinese remainder theorem.