Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
| # | User | Rating |
|---|---|---|
| 1 | ecnerwala | 3649 |
| 2 | Benq | 3581 |
| 3 | orzdevinwang | 3570 |
| 4 | Geothermal | 3569 |
| 4 | cnnfls_csy | 3569 |
| 6 | tourist | 3565 |
| 7 | maroonrk | 3531 |
| 8 | Radewoosh | 3521 |
| 9 | Um_nik | 3482 |
| 10 | jiangly | 3468 |
| # | User | Contrib. |
|---|---|---|
| 1 | maomao90 | 174 |
| 2 | awoo | 164 |
| 3 | adamant | 161 |
| 4 | TheScrasse | 159 |
| 5 | nor | 158 |
| 6 | maroonrk | 156 |
| 7 | -is-this-fft- | 152 |
| 8 | SecondThread | 147 |
| 9 | orz | 146 |
| 10 | pajenegod | 145 |
| Name |
|---|



It was hard to see that D can't be solved with Rho, and I've seen a problem like G before (so I knew what ifs are needed). Other than that, nice problems! E was very very cool.
Thanks!
I was worried that D would be solvable by Rho, but tests suggested that it just wasn't. It's difficult to rely on algorithm with unproved complexity.
Random question from a person who's not an expert in fancy factorization algorithms: can we get stuff done by using something more advanced than algorithms typically used in competitive programming (like it has been indirectly suggested in this comment), and if we can — do you have any information about contestants actually doing so? Was it a popular approach or not? :)
We can use Shank's SQUFOF. It factors N in around O(N1 / 4), but its main advantage is that SQUFOF doesn't need 128-bit multiplication and uses only 32-bit integers for the most part.
I don't fully understand the algorithm and the implementation needs quite a few tricks to even work at all, but it is really fast, passing in 62 ms.
Please don't do that. I would have to set ai ≤ 10100 next time :)
Personally, I thought the bad performance of Rho is due to the huge amount of calls to gcd function, which may cause the time complexity to become . However, it can be optimized if you adjust that to call gcd function once during a considerable period. Besides, a fast algorithm for modular multiplication such as Montgomery Modular Multiplication may help a lot.
. However, it can be optimized if you adjust that to call gcd function once during a considerable period. Besides, a fast algorithm for modular multiplication such as Montgomery Modular Multiplication may help a lot.
Maybe an accepted solution of Rho: 43964647
I wish u gonna discuss those in next live stream.
When will the problems be available in practice
Shortly after system test finishes.
Why did you cut the limit to 20000 on E? Is it because of the time limits or are you afraid that some solutions with bad asymptotic could pass? To me, i think that it would be cool if solutions with correct asymptotic and bad constants could pass too.
To me solution described in editorial sounds like the one having bad constant :)
One can find a spanning tree by running DFS from any vertex. We can implement a function "find if there is an edge from v to unused vertex" using trick from the first paragraph, but with only 2 queries instead of 3 (your set A consists of single vertex, so you know that e(A) is equal to 0). Now let's wrap it with binary search: first you check that at least one edge exists (asking it against whole set of unused vertices), and then you can bisect with one call of our function instead of two: split your set into two parts and check if there is a good edge in one of them; if it is not there, we know for sure that it is in the other part. It means that we'll do roughly N * log(N) + N calls of helper function, and each such call is 2 interactive queries. Therefore we can estimate that we are somewhere at 12-13k queries worst case (sorry, I'm lazy to actually calculate it precisely), which is significantly better than 20k.
So this problem actually doesn't look bad in terms of constants; it is way better than typical "You are allowed to perform at most 73 queries (so now you know how many queries model solution will need)".
One can do bipartite check using the same idea; then, caching is not needed at all.
The solution passes all tests with ~11k queries.
thank you very much for this contest it was very good but i solved ( b ) problem only i wish to be good in the future like you and other professional contestant
Nice Contest this!!!!
My Solution of problem D couldn't able to pass the sys-test as I have used Shanks's square forms factorization to get one prime p from the form p*q. It returns wrong output for the number 1184554290421768229. Can anyone enlighten me about this bug? Actually I have copied the exact code from wiki for this algorithm and it produces wrong output. So is it happening because of the code or the algorithm itself has some bugs?
You get a runtime error. Perhaps some undefined behaviour in your code? If you resubmit with "Clang diagnostics" compiler, you might get some more information.
Actually, the Shanks algorithm is producing 0 even if it is taking a semiprime as an input. I think the algorithm has some bug in it. I am not using it anymore in future or if you have some better implementation of this algorithm I could use that in the future.
Your code has a few issues.
and
for example).
coarse_cutoffandcutoff(Just note that the msieve code fails for n = p3.). My implementation is based on that code and the cutoff part makes a huge difference. (Your code fails on 422497460091096893 = 481512587·877438039 and 51104449379303477 = 656561·77836559557.)Here's the code I used to generate the above test cases (I ran it with T ≈ 15'000).
Thanks for your reply. I have learnt so many things from you today. And I will use your code in future for factorizing large numbers and that cool SQUFOF algorithm. And again, thanks.
In problem C , can any one tell me what's wrong on my approach ? why does it give wrong answer on Test 23 ?
http://codeforces.com/contest/1033/submission/43970251
I solved it with DP , states are <CurrentNodeValue , Turn > , Current State is to pick the optimal choice depends on transitions (For example :- currentTurn for Alice , Alice must search for any odd moves to Win and Bob must search for even moves to Win )
Related to D: what about pq^2, p^2q and p^2q^2 forms?
pq2 has six divisors (1, p, q, pq, q2 and pq2), so it cannot be part of the input.
Thanks.
How did you implement the interactor in E? What is the complexity of answering each query? I cannot see any method better than the naive O(n2) per query which will simply TLE.
I think optimizing the intersection count with bitset should be enough.
can you please elaborate a little?
Refer to the interactor.
infis a stream reading from the file describing the test case (i.e. a graph)coutis an output stream towards the solution (this is the input you're reading from)oufis an input stream towards the solution (this is the output you're printing)toutis the log written by the interactor. Afterwards, it is fed to the checker.Eis the adjacency matrixFis the bitset representing the querythanks for the reply! Can you please also answer this or provide an implementation based on the editorial.
Can anyone explain me problem C ?
I'll try to explain my approach for the problem.
It makes use of game theory. Game theory states that "if I am currently at X, and if I can move to states Y1, Y2 .. YK, if each of the state Y1, Y2 .. YK are winning states for me(i.e., if I would win the game if I was at Y1 or Y2 or YK..), then X is a losing state for me. If any one of Y1 or Y2 or .. YK was a losing state for me, then X is a winning state for me.
Fill an array with values 1 if Alice has a winning position if she starts at i, else 0.
So we can just fill the array from N to 1. for each value, go to all possible states where she can move next ( I — I, I — 2I, I — 3I , I+I, I+2I etc.) and check if any of those had values 0. If yes, I is a winning state for us. Else, I is a losing state.
Complexity should be similar to that of Sieve, i.e, N * log (N)
Code: 44012560
Can you explain the time complexity , why it is nlog(n)
The second approach of F can be implemented in O(n + 3w + m·2w) time.
Hello. I have been trying Problem D with the same approach as above,but getting WA on test case 15. Can someone help me out?? Here's the link: https://codeforces.com/contest/1033/submission/43976266
It is due to errors in accuracy. I got WA on the same test case and I therefore had to check within +-1 of the obtained sqrt (and for other powers too). For example I guess sometimes when the actual sqrt is say 100000, the sqrt function in c++ might return 99999.999 and since this gets rounded down, you lose out on accuracy. I hope you got the point.
Thank You.It worked!!
can we trust on pow(n,0.5) instead of sqrt(n) ? or we have to make our own function for calculating powers ?
I replaced sqrt with sqrtl and cbrt with cbrtl and my solution got Accepted.
facepalm btw you replaced sqrt with sqrt(sqrtl)
In problem E can someone please help me to optimize my solution? I did the same as mentioned in editorial.
can someone please give link to the code of the solution mentioned in the editorial.
In Problem F, the complexity O(w·3w) in one step is O(3w) in fact.
When we calculate f(i, s, t): how many number satisfying that first i bits are equal to s, and last w - i bits matches t (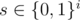 ,
, 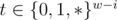 ), the total complexity is
), the total complexity is
In Problem G, we only need to split the number into 2 parts: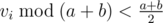 and
and 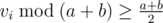 , and then get the maximum number of the first part, the size, the maximum two numbers and the minimum number of the second part, then discuss some cases like the editiorial. It can get rid of the log factor.
, and then get the maximum number of the first part, the size, the maximum two numbers and the minimum number of the second part, then discuss some cases like the editiorial. It can get rid of the log factor.
in B , i am doing in O(sqrt(a+b)) time approx 10^5 operations ,but gives tle why??
The line to blame is
for(int i=2;i*i<=a ;i++)Since
intis 32-bit, you have an overflow when computingi*i. If a is larger than 231 (which it can be), the condition is always true, hence the infinite loop.i got it ..thanku so much..
please suggest me some ways how to practice competitive problems so that i can do D or E level problems..refer any link or share the way you did in beginning..
Keep solving lots of problems.
Solve something just outside of your comfort zone, so you can keep expanding it.
If you can't solve something after a lot of effort, read the editorial. Most important is not to just understand the solution, but to reflect on WHY you didn't come up with the solution, and how you could have got that solution if you were to do the problem over again. Make sure that next time you need a similar technique you won't miss it.
Keep doing that and you will get better and better over time. There's no easy way but the journey is lots of fun.
Hello all, my code gives correct answer for CASE 4 (Problem D) in local machine but here it fails. Can someone help me with this. Link for submission: code
I have a doubt in Problem C Test Case 8:
40
5 40 6 27 39 37 17 34 3 30 28 13 12 8 11 10 31 4 1 16 38 22 29 35 33 23 7 9 24 14 18 26 19 21 15 36 2 20 32 25
ANSWER : ABABBBABABAAAAAABAAABBBBBBAAAABABBABABBB
index = 40 -> ans = B
index = 10 -> ans = B
Shouldn't answer for index 10 be A i.e opposite of its reacheable index(i.e 40).
As 25 < 30, you cannot move the token from 30 to 25. There are thus no valid moves from 30, and Bob wins.
Thanks Sir, Finally got a AC. I just overlooked that condition.
Can someone tell at why 77478143 this code is failing. I am using DP with greedy and I am unable to figure out where it is failing.
for problem C
In problem C, can someone prove that $$$\sum\limits_{i = 1}^n\lfloor{n/i}\rfloor$$$ is of order $$$O(n\log{n})$$$?
Does anyone here has used DFS in 1033A.
Any DFS/BFS solution for A?