A histogram is a polygon made by aligning $$$N$$$ adjacent rectangles that share a common base line. Each rectangle is called a bar. The $$$i$$$-th bar from the left has width 1 and height $$$H_i$$$.
Your goal is to find the area of the largest rectangle contained in the given histogram, such that one of the sides is parallel to the base line.
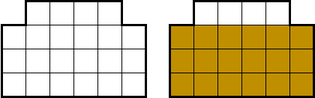
Figure 1. The histogram given in the example, with the largest rectangle shown on the right.
Actually, no, you have to find the largest square. Since the area of a square is determined by its side length, you are required to output the side length instead of the area.

Figure 2. The histogram given in the example, with the largest square shown on the right.
On the first line, a single integer $$$N$$$ is given, where $$$1 \le N \leq 300\,000$$$.
On the next line, $$$N$$$ space-separated integers $$$H_1, H_2, \cdots, H_N$$$, are given. $$$H_i$$$ $$$(1 \le H_i \le 10^9)$$$ is the height of the $$$i$$$-th bar.
Output the side length of the largest square in the histogram, such that one of the sides is parallel to the base line.
6 3 4 4 4 4 3
4
| Name |
|---|




