You are given a rooted tree with $$$n$$$ nodes, labeled from $$$1$$$ to $$$n$$$. The tree is rooted at node $$$1$$$. The parent of the $$$i$$$-th node is $$$p_i$$$. A leaf is node with no children. For a given set of leaves $$$L$$$, let $$$f(L)$$$ denote the smallest connected subgraph that contains all leaves $$$L$$$.
You would like to partition the leaves such that for any two different sets $$$x, y$$$ of the partition, $$$f(x)$$$ and $$$f(y)$$$ are disjoint.
Count the number of ways to partition the leaves, modulo $$$998244353$$$. Two ways are different if there are two leaves such that they are in the same set in one way but in different sets in the other.
The first line contains an integer $$$n$$$ ($$$2 \leq n \leq 200\,000$$$) — the number of nodes in the tree.
The next line contains $$$n-1$$$ integers $$$p_2, p_3, \ldots, p_n$$$ ($$$1 \leq p_i < i$$$).
Print a single integer, the number of ways to partition the leaves, modulo $$$998244353$$$.
5 1 1 1 1
12
10 1 2 3 4 5 6 7 8 9
1
In the first example, the leaf nodes are $$$2,3,4,5$$$. The ways to partition the leaves are in the following image 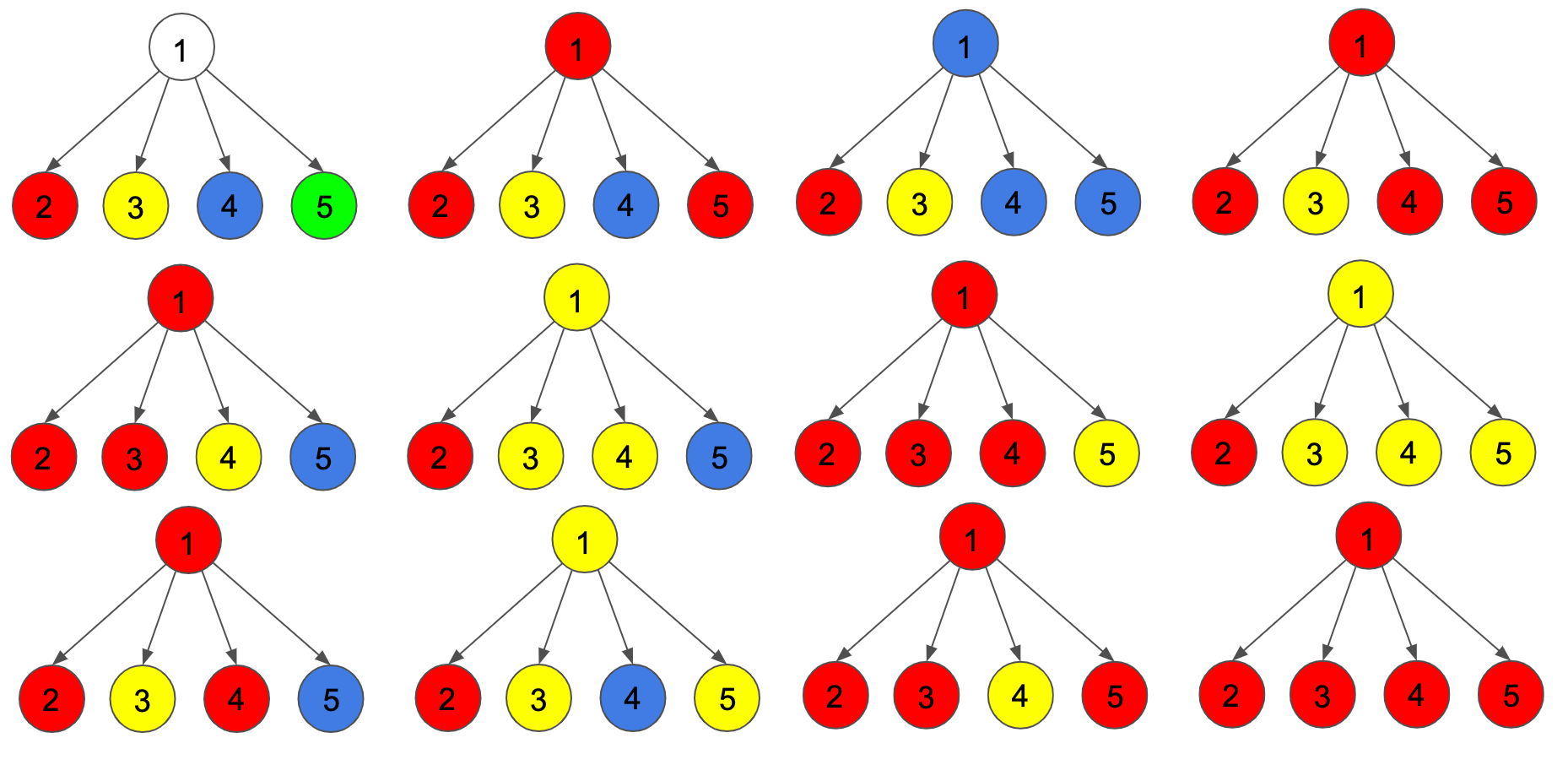
In the second example, the only leaf is node $$$10$$$ so there is only one partition. Note that node $$$1$$$ is not a leaf.
| Name |
|---|




