| Codeforces Round 558 (Div. 2) |
|---|
| Finished |
This problem is same as the previous one, but has larger constraints.
It was a Sunday morning when the three friends Selena, Shiro and Katie decided to have a trip to the nearby power station (do not try this at home). After arriving at the power station, the cats got impressed with a large power transmission system consisting of many chimneys, electric poles, and wires. Since they are cats, they found those things gigantic.
At the entrance of the station, there is a map describing the complicated wiring system. Selena is the best at math among three friends. He decided to draw the map on the Cartesian plane. Each pole is now a point at some coordinates $$$(x_i, y_i)$$$. Since every pole is different, all of the points representing these poles are distinct. Also, every two poles are connected with each other by wires. A wire is a straight line on the plane infinite in both directions. If there are more than two poles lying on the same line, they are connected by a single common wire.
Selena thinks, that whenever two different electric wires intersect, they may interfere with each other and cause damage. So he wonders, how many pairs are intersecting? Could you help him with this problem?
The first line contains a single integer $$$n$$$ ($$$2 \le n \le 1000$$$) — the number of electric poles.
Each of the following $$$n$$$ lines contains two integers $$$x_i$$$, $$$y_i$$$ ($$$-10^4 \le x_i, y_i \le 10^4$$$) — the coordinates of the poles.
It is guaranteed that all of these $$$n$$$ points are distinct.
Print a single integer — the number of pairs of wires that are intersecting.
4 0 0 1 1 0 3 1 2
14
4 0 0 0 2 0 4 2 0
6
3 -1 -1 1 0 3 1
0
In the first example:

In the second example:
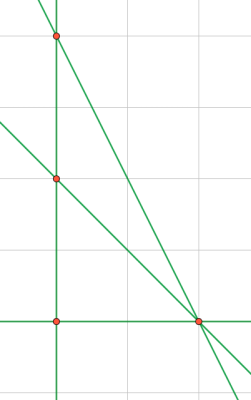
Note that the three poles $$$(0, 0)$$$, $$$(0, 2)$$$ and $$$(0, 4)$$$ are connected by a single wire.
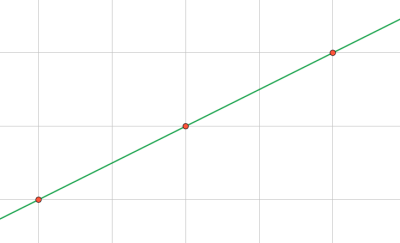
In the third example:
| Name |
|---|




