| Codeforces Round 589 (Div. 2) |
|---|
| Finished |
→ Virtual participation
Virtual contest is a way to take part in past contest, as close as possible to participation on time. It is supported only ICPC mode for virtual contests.
If you've seen these problems, a virtual contest is not for you - solve these problems in the archive.
If you just want to solve some problem from a contest, a virtual contest is not for you - solve this problem in the archive.
Never use someone else's code, read the tutorials or communicate with other person during a virtual contest.
→ Problem tags
combinatorics
dp
math
*2300
No tag edit access
→ Contest materials
The problem statement has recently been changed. View the changes.
×
E. Another Filling the Grid
time limit per test
1 secondmemory limit per test
256 megabytesinput
standard inputoutput
standard outputYou have $$$n \times n$$$ square grid and an integer $$$k$$$. Put an integer in each cell while satisfying the conditions below.
- All numbers in the grid should be between $$$1$$$ and $$$k$$$ inclusive.
- Minimum number of the $$$i$$$-th row is $$$1$$$ ($$$1 \le i \le n$$$).
- Minimum number of the $$$j$$$-th column is $$$1$$$ ($$$1 \le j \le n$$$).
Find the number of ways to put integers in the grid. Since the answer can be very large, find the answer modulo $$$(10^{9} + 7)$$$.
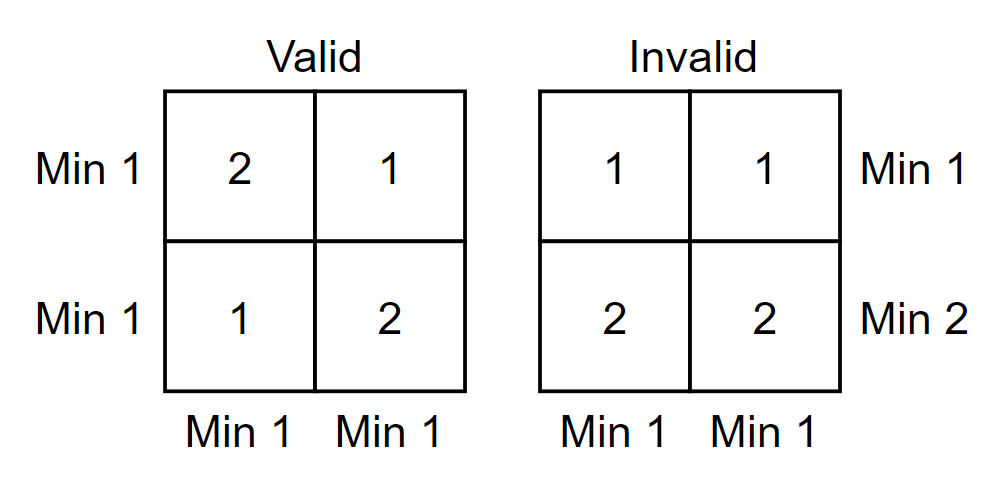 These are the examples of valid and invalid grid when $$$n=k=2$$$.
These are the examples of valid and invalid grid when $$$n=k=2$$$. Input
The only line contains two integers $$$n$$$ and $$$k$$$ ($$$1 \le n \le 250$$$, $$$1 \le k \le 10^{9}$$$).
Output
Print the answer modulo $$$(10^{9} + 7)$$$.
Examples
Input
2 2
Output
7
Input
123 456789
Output
689974806
Note
In the first example, following $$$7$$$ cases are possible.
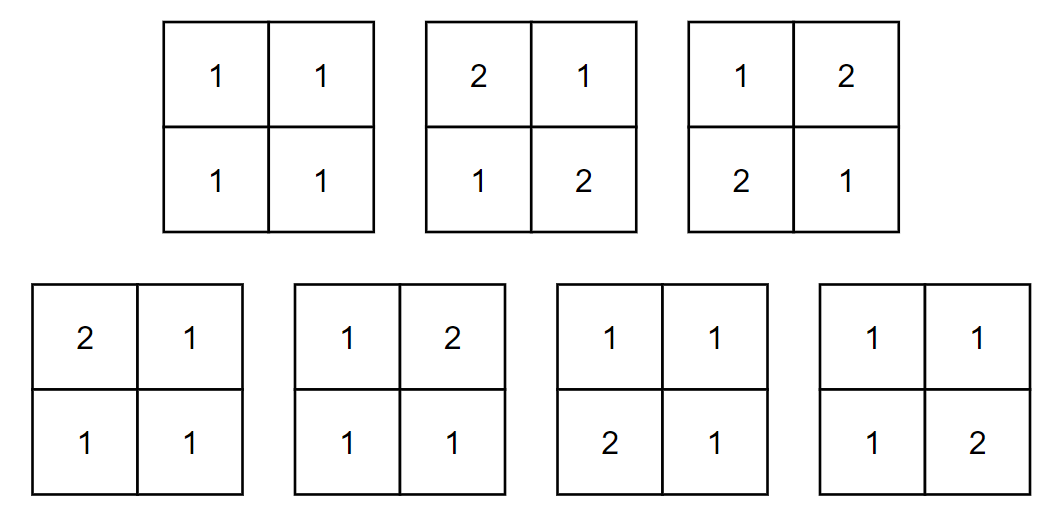
In the second example, make sure you print the answer modulo $$$(10^{9} + 7)$$$.
Codeforces (c) Copyright 2010-2024 Mike Mirzayanov
The only programming contests Web 2.0 platform
Server time: Jul/28/2024 12:17:25 (i1).
Desktop version, switch to mobile version.
Supported by
User lists


| Name |
|---|




