| Codeforces Round 589 (Div. 2) |
|---|
| Finished |
You have an integer $$$n$$$. Let's define following tree generation as McDic's generation:
- Make a complete and full binary tree of $$$2^{n} - 1$$$ vertices. Complete and full binary tree means a tree that exactly one vertex is a root, all leaves have the same depth (distance from the root), and all non-leaf nodes have exactly two child nodes.
- Select a non-root vertex $$$v$$$ from that binary tree.
- Remove $$$v$$$ from tree and make new edges between $$$v$$$'s parent and $$$v$$$'s direct children. If $$$v$$$ has no children, then no new edges will be made.
You have a tree. Determine if this tree can be made by McDic's generation. If yes, then find the parent vertex of removed vertex in tree.
The first line contains integer $$$n$$$ ($$$2 \le n \le 17$$$).
The $$$i$$$-th of the next $$$2^{n} - 3$$$ lines contains two integers $$$a_{i}$$$ and $$$b_{i}$$$ ($$$1 \le a_{i} \lt b_{i} \le 2^{n} - 2$$$) — meaning there is an edge between $$$a_{i}$$$ and $$$b_{i}$$$. It is guaranteed that the given edges form a tree.
Print two lines.
In the first line, print a single integer — the number of answers. If given tree cannot be made by McDic's generation, then print $$$0$$$.
In the second line, print all possible answers in ascending order, separated by spaces. If the given tree cannot be made by McDic's generation, then don't print anything.
4 1 2 1 3 2 4 2 5 3 6 3 13 3 14 4 7 4 8 5 9 5 10 6 11 6 12
1 3
2 1 2
2 1 2
3 1 2 2 3 3 4 4 5 5 6
0
In the first example, $$$3$$$ is the only possible answer.
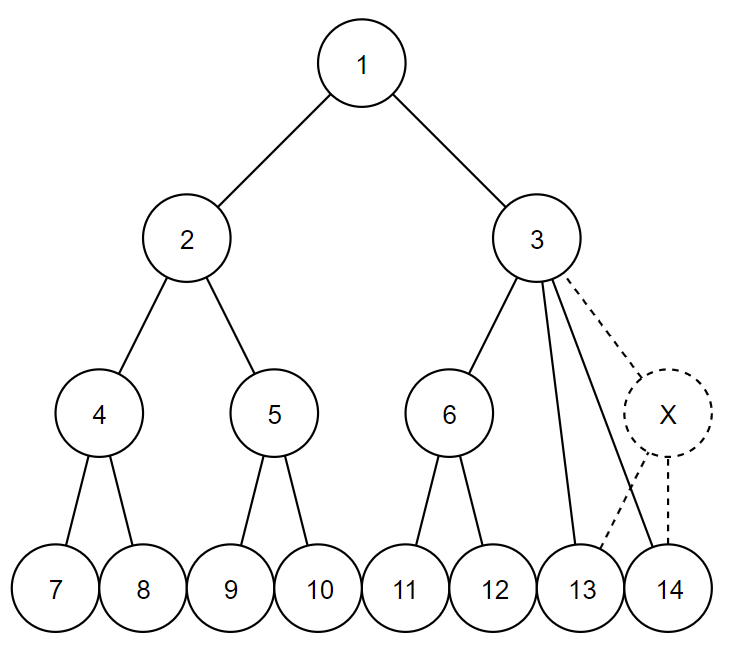
In the second example, there are $$$2$$$ possible answers.

In the third example, the tree can't be generated by McDic's generation.
| Name |
|---|




