В мире есть $$$n$$$ футбольных команд.
Главная футбольная организация (ГФО) хочет провести не более $$$m$$$ игр. ГФО хочет, чтобы $$$i$$$-я игра была сыграна между командами $$$a_i$$$ и $$$b_i$$$ на одном из $$$k$$$ стадионов.
Пусть $$$s_{ij}$$$ будет количеством игр, которые сыграла $$$i$$$-я команда на $$$j$$$-м стадионе. ГФО не хочет, чтобы какая-то команда сыграла на много больше матчей на одному стадионе, чем на каком-то другом. Поэтому, для каждой команды $$$i$$$, абсолютная разница между максимом и минимум среди чисел $$$s_{i1}, s_{i2}, \ldots, s_{ik}$$$ не должна превосходить $$$2$$$.
Каждая команда имеет $$$w_i$$$ — количество денег, которые получит ГФО за каждую игру $$$i$$$-й команды. Если $$$i$$$-я команда сыграет $$$l$$$ матчей, то ГФО заработает $$$w_i \cdot l$$$.
ГФО нужно найти какие игры и на каких стадионах нужно сыграть, чтобы они заработали как можно больше денег, но при этом не нарушая правила, которые они установили.
К сожалению, эта задача слишком сложная для ГФО. Поэтому они просят вас решить эту задачу.
Первая строка содержит три целых числа $$$n$$$, $$$m$$$, $$$k$$$ ($$$3 \leq n \leq 100$$$, $$$0 \leq m \leq 1\,000$$$, $$$1 \leq k \leq 1\,000$$$) — количество команд, количество игр и количество стадионов.
Вторая строка содержит $$$n$$$ целых чисел $$$w_1, w_2, \ldots, w_n$$$ ($$$1 \leq w_i \leq 1\,000$$$) — количество денег, которое получит ГФО за каждую игру $$$i$$$-й команды.
Каждая из следующих $$$m$$$ строк содержит два целых числа $$$a_i$$$ и $$$b_i$$$ ($$$1 \leq a_i, b_i \leq n$$$, $$$a_i \neq b_i$$$) — команды, которые могут сыграть $$$i$$$-ю игру. Гарантируется, что каждая пара команд может сыграть не более одной игры.
Для каждой игры в том же порядке выведите $$$t_i$$$ ($$$1 \leq t_i \leq k$$$) — номер стадиона, на котором команды $$$a_i$$$ и $$$b_i$$$ сыграют игру. Если $$$i$$$-я игра не должна быть сыграна, то $$$t_i$$$ должен быть равен $$$0$$$.
Если существует несколько решений, выведите любое из них.
7 11 3 4 7 8 10 10 9 3 6 2 6 1 7 6 4 3 4 6 3 1 5 3 7 5 7 3 4 2 1 4
3 2 1 1 3 1 2 1 2 3 2
Один из возможных решений примера показан ниже:
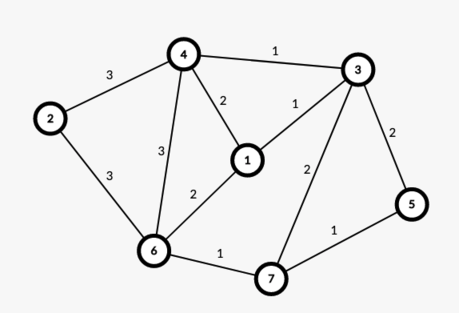
| Название |
|---|




