| Codeforces Round 599 (Div. 1) |
|---|
| Finished |
Ujan has a lot of useless stuff in his drawers, a considerable part of which are his math notebooks: it is time to sort them out. This time he found an old dusty graph theory notebook with a description of a graph.
It is an undirected weighted graph on $$$n$$$ vertices. It is a complete graph: each pair of vertices is connected by an edge. The weight of each edge is either $$$0$$$ or $$$1$$$; exactly $$$m$$$ edges have weight $$$1$$$, and all others have weight $$$0$$$.
Since Ujan doesn't really want to organize his notes, he decided to find the weight of the minimum spanning tree of the graph. (The weight of a spanning tree is the sum of all its edges.) Can you find the answer for Ujan so he stops procrastinating?
The first line of the input contains two integers $$$n$$$ and $$$m$$$ ($$$1 \leq n \leq 10^5$$$, $$$0 \leq m \leq \min(\frac{n(n-1)}{2},10^5)$$$), the number of vertices and the number of edges of weight $$$1$$$ in the graph.
The $$$i$$$-th of the next $$$m$$$ lines contains two integers $$$a_i$$$ and $$$b_i$$$ ($$$1 \leq a_i, b_i \leq n$$$, $$$a_i \neq b_i$$$), the endpoints of the $$$i$$$-th edge of weight $$$1$$$.
It is guaranteed that no edge appears twice in the input.
Output a single integer, the weight of the minimum spanning tree of the graph.
6 11 1 3 1 4 1 5 1 6 2 3 2 4 2 5 2 6 3 4 3 5 3 6
2
3 0
0
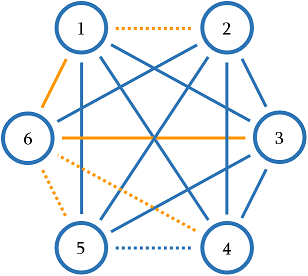
The graph from the first sample is shown below. Dashed edges have weight $$$0$$$, other edges have weight $$$1$$$. One of the minimum spanning trees is highlighted in orange and has total weight $$$2$$$.
In the second sample, all edges have weight $$$0$$$ so any spanning tree has total weight $$$0$$$.
| Name |
|---|




